4. Evaluation Metrics for Classification¶
Last week we trained a model for churn. How do we know if it’s good?
The fourth week of Machine Learning Zoomcamp is about different metrics to evaluate a binary classifier. These measures include accuracy, confusion table, precision, recall, ROC curves(TPR, FRP, random model, and ideal model), AUROC, and cross-validation.
4.1 Evaluation metrics: session overview¶
- Dataset: https://www.kaggle.com/blastchar/telco-customer-churn
- https://raw.githubusercontent.com/alexeygrigorev/mlbookcamp-code/master/chapter-03-churn-prediction/WA_Fn-UseC_-Telco-Customer-Churn.csv
Metric – function that compares the predictions with the actual values and outputs a single number that tells how good the predictions are
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction import DictVectorizer
from sklearn.linear_model import LogisticRegression
import urllib.request
url = 'https://raw.githubusercontent.com/alexeygrigorev/mlbookcamp-code/master/chapter-03-churn-prediction/WA_Fn-UseC_-Telco-Customer-Churn.csv'
filename = 'data-week-3.csv'
df = pd.read_csv(url)
df.columns = df.columns.str.lower().str.replace(' ', '_')
categorical_columns = list(df.dtypes[df.dtypes == 'object'].index)
for c in categorical_columns:
df[c] = df[c].str.lower().str.replace(' ', '_')
df.totalcharges = pd.to_numeric(df.totalcharges, errors='coerce')
df.totalcharges = df.totalcharges.fillna(0)
df.churn = (df.churn == 'yes').astype(int)
df_full_train, df_test = train_test_split(df, test_size=0.2, random_state=1)
df_train, df_val = train_test_split(df_full_train, test_size=0.25, random_state=1)
df_train = df_train.reset_index(drop=True)
df_val = df_val.reset_index(drop=True)
df_test = df_test.reset_index(drop=True)
y_train = df_train.churn.values
y_val = df_val.churn.values
y_test = df_test.churn.values
del df_train['churn']
del df_val['churn']
del df_test['churn']
numerical = ['tenure', 'monthlycharges', 'totalcharges']
categorical = [
'gender',
'seniorcitizen',
'partner',
'dependents',
'phoneservice',
'multiplelines',
'internetservice',
'onlinesecurity',
'onlinebackup',
'deviceprotection',
'techsupport',
'streamingtv',
'streamingmovies',
'contract',
'paperlessbilling',
'paymentmethod',
]
dv = DictVectorizer(sparse=False)
train_dict = df_train[categorical + numerical].to_dict(orient='records')
X_train = dv.fit_transform(train_dict)
model = LogisticRegression()
model.fit(X_train, y_train)
LogisticRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LogisticRegression()
val_dict = df_val[categorical + numerical].to_dict(orient='records')
X_val = dv.transform(val_dict)
y_pred = model.predict_proba(X_val)[:, 1]
churn_decision = (y_pred >= 0.5)
(y_val == churn_decision).mean()
0.8034066713981547
4.2 Accuracy and dummy model¶
Accurcy measures the fraction of correct predictions. Specifically, it is the number of correct predictions divided by the total number of predictions.
We can change the decision threshold, it should not be always 0.5. But, in this particular problem, the best decision cutoff, associated with the hightest accuracy (80%), was indeed 0.5.
Note that if we build a dummy model in which the decision cutoff is 1, so the algorithm predicts that no clients will churn, the accuracy would be 73%. Thus, we can see that the improvement of the original model with respect to the dummy model is not as high as we would expect.
Therefore, in this problem accuracy can not tell us how good is the model because the dataset is unbalanced, which means that there are more instances from one category than the other. This is also known as class imbalance.
Classes and methods:
np.linspace(x,y,z)– returns a numpy array starting at x until y with a z stepCounter(x)– collection class that counts the number of instances that satisfy the x conditionaccuracy_score(x, y)– sklearn.metrics class for calculating the accuracy of a model, given a predicted x dataset and a target y dataset.
len(y_val)
1409
(y_val == churn_decision).sum() / len(y_val)
0.8034066713981547
So we have the accuracy of our base model using 0.5 as the cutoff for churn, no churn. Now we will vary the 0.5 to different numbers to see if the accuracy of our model is better or not.
The np.linspace() method can be used to create an array. In this case we want the values in the array to be from 0 to 1 and we want 21 of them. That will start at 0 and increment by .05 each step.
thresholds = np.linspace(0, 1, 21)
thresholds
array([0. , 0.05, 0.1 , 0.15, 0.2 , 0.25, 0.3 , 0.35, 0.4 , 0.45, 0.5 ,
0.55, 0.6 , 0.65, 0.7 , 0.75, 0.8 , 0.85, 0.9 , 0.95, 1. ])
scores = []
for t in thresholds:
churn_decision = (y_pred >= t)
score = (y_val == churn_decision).mean()
print('%.2f %.3f' % (t, score))
scores.append(score)
0.00 0.274 0.05 0.510 0.10 0.591 0.15 0.666 0.20 0.710 0.25 0.739 0.30 0.760 0.35 0.772 0.40 0.785 0.45 0.793 0.50 0.803 0.55 0.801 0.60 0.796 0.65 0.786 0.70 0.766 0.75 0.744 0.80 0.734 0.85 0.726 0.90 0.726 0.95 0.726 1.00 0.726
plt.plot(thresholds, scores)
[<matplotlib.lines.Line2D at 0x29303c8cd30>]
We can see that 0.5 is the best one. We used our own function for calculating accuracy (y_val == churn_decision).mean(). sklearn has a function for accuracy, accuracy_score. Let’s implement that.
from sklearn.metrics import accuracy_score
accuracy_score(y_val, y_pred >= 0.5)
0.8034066713981547
Let’s add that into our previous function to calculate accuracy with the thresholds array.
scores = []
for t in thresholds:
score = accuracy_score(y_val, y_pred >= t)
print('%.2f %.3f' % (t, score))
scores.append(score)
0.00 0.274 0.05 0.510 0.10 0.591 0.15 0.666 0.20 0.710 0.25 0.739 0.30 0.760 0.35 0.772 0.40 0.785 0.45 0.793 0.50 0.803 0.55 0.801 0.60 0.796 0.65 0.786 0.70 0.766 0.75 0.744 0.80 0.734 0.85 0.726 0.90 0.726 0.95 0.726 1.00 0.726
plt.plot(thresholds, scores)
[<matplotlib.lines.Line2D at 0x29303cd7730>]
At the threshold of 1.0 we can see our prediction rate is 72.6%. That must mean that our churn rate in the validation set is 72.6%. Let’s verify that using the Counter method, which simply counts the number of True or False.
from collections import Counter
Counter(y_pred >= 1.0)
Counter({False: 1409})
As we can see the number of False records is at 1409, which is the size of our array, so none of the values are greater than 1. Below we can simply do a small calculation and see that it is simply a calculation of the churn rate of our dataset.
1 - y_val.mean()
0.7260468417317246
So the actual non churn rate is at 72.6% for the validation dataset and our model is only 7.4% better. So accuracy isn’t the best choice for scoring our model. This is because we have what is called class imbalance. We have 72.6% of customers that don’t churn compared to 27.4% of customers that do churn.
y_val.mean()
0.2739531582682754
4.3 Confusion table¶
Confusion table is a way to measure different types of errors and correct decisions that binary classifiers can made. Considering this information, it is possible evaluate the quality of the model by different strategies.
If we predict the probability of churning from a customer, we have the following scenarios:
- No churn – Negative class
- Customer did not churn – True Negative (TN)
- Customer churned – False Negative (FN)
- Churn – Positive class
- Customer churned – True Positive (TP)
- Customer did not churn – False Positive (FP)
The confusion table help us to summarize the measures explained above in a tabular format, as is shown below:
| Actual/Predictions | Negative | Postive |
|---|---|---|
| Negative | TN | FP |
| Postive | FN | TP |
The accuracy corresponds to the sum of TN and TP divided by the total of observations.
actual_positive = (y_val == 1)
actual_negative = (y_val == 0)
actual_positive, actual_negative
(array([False, False, False, ..., False, True, True]), array([ True, True, True, ..., True, False, False]))
t = 0.5
predict_positive = (y_pred >= t)
predict_negative = (y_pred < t)
predict_positive, predict_negative
(array([False, False, False, ..., False, True, True]), array([ True, True, True, ..., True, False, False]))
In effect, what we are setting up is a logic AND argument. If both are True then the output is True, if both are False then the output is True, if either is different then we get an output that is False
predict_positive & actual_positive
array([False, False, False, ..., False, True, True])
(predict_positive & actual_positive).sum()
210
We have 210 True Positives and 922 True Negatives
tp = (predict_positive & actual_positive).sum()
tn = (predict_negative & actual_negative).sum()
tp, tn
(210, 922)
We have 101 False Positives and 176 False Negatives
fp = (predict_positive & actual_negative).sum()
fn = (predict_negative & actual_positive).sum()
fp, fn
(101, 176)
confusion_matrix = np.array([
[tn, fp],
[fn, tp]
])
confusion_matrix
array([[922, 101],
[176, 210]])
What all of this is telling us is that with our current model we would be sending out 101 discount emails to people who not at risk of churning and we would be missing out by not sending out 176 discount emails to people who were going to churn. In the first case we are losing money because we gave discounts to people who were not at risk of churning and in the second case we are missing out on future money by not attempting to retain customers that are at high risk for churning.
(confusion_matrix / confusion_matrix.sum()).round(2)
array([[0.65, 0.07],
[0.12, 0.15]])
4.4 Precision and Recall¶
Precision tell us the fraction of positive predictions that are correct. It takes into account only the positive class (TP and FP – second column of the confusion matrix), as is stated in the following formula:
TP / (TP + FP)
Recall measures the fraction of correctly identified postive instances. It considers parts of the postive and negative classes (TP and FN – second row of confusion table). The formula of this metric is presented below:
TP / (TP + FN)
In this problem, the precision and recall values were 67% and 54% respectively. So, these measures reflect some errors of our model that accuracy did not notice due to the class imbalance.
Precision¶
(tp + tn) / (tp + tn + fp + fn) # accuracy score of our model
0.8034066713981547
In the precision score we are only interested in scores that equal churn. In this case we would be interested in the TP and FP.
p = tp / (fp + tp)
p
0.6752411575562701
Recall¶
r = tp / (tp + fn)
r
0.5440414507772021
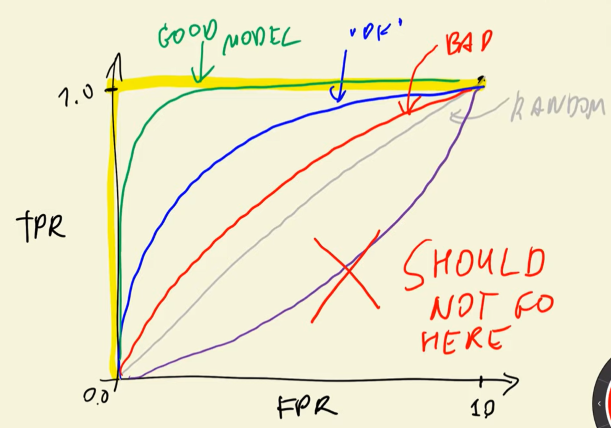
4.5 ROC Curves¶
ROC stands for Receiver Operating Characteristic, and this idea was applied during the Second World War for evaluating the strenght of radio detectors. This measure considers False Positive Rate (FPR) and True Postive Rate (TPR), which are derived from the values of the confusion matrix.
FPR is the fraction of false positives (FP) divided by the total number of negatives (FP and TN – the first row of confusion matrix), and we want to minimize it. The formula of FPR is the following:
In the other hand, TPR or Recall is the fraction of true positives (TP) divided by the total number of positives (FN and TP – second row of confusion table), and we want to maximize this metric. The formula of this measure is presented below:
ROC curves consider Recall and FPR under all the possible thresholds. If the threshold is 0 or 1, the TPR and Recall scores are the opposite of the threshold (1 and 0 respectively), but they have different meanings, as we explained before.
We need to compare the ROC curves against a point of reference to evaluate its performance, so the corresponding curves of random and ideal models are required. It is possible to plot the ROC curves with FPR and Recall scores vs thresholds, or FPR vs Recall.
Classes and methods:
np.repeat([x,y], [z,w])– returns a numpy array with a z number of x values, and a w number of y values.roc_curve(x, y)– sklearn.metrics class for calculating the false positive rates, true positive rates, and thresholds, given a target x dataset and a predicted y dataset.
TPR and FPR¶
TPR is the same equation as recall
tpr = tp / (fn + tp)
tpr
0.5440414507772021
fpr = fp / (tn + fp)
fpr
0.09872922776148582
scores = []
thresholds = np.linspace(0, 1, 101)
for t in thresholds:
actual_positive = (y_val == 1)
actual_negative = (y_val == 0)
predict_positive = (y_pred >= t)
predict_negative = (y_pred < t)
tp = (predict_positive & actual_positive).sum()
tn = (predict_negative & actual_negative).sum()
fp = (predict_positive & actual_negative).sum()
fn = (predict_negative & actual_positive).sum()
scores.append((t, tp, fp, fn, tn))
scores
[(0.0, 386, 1023, 0, 0), (0.01, 385, 914, 1, 109), (0.02, 384, 830, 2, 193), (0.03, 383, 766, 3, 257), (0.04, 381, 715, 5, 308), (0.05, 379, 683, 7, 340), (0.06, 377, 661, 9, 362), (0.07, 372, 640, 14, 383), (0.08, 371, 613, 15, 410), (0.09, 369, 580, 17, 443), (0.1, 366, 556, 20, 467), (0.11, 365, 528, 21, 495), (0.12, 365, 509, 21, 514), (0.13, 360, 477, 26, 546), (0.14, 355, 453, 31, 570), (0.15, 351, 435, 35, 588), (0.16, 347, 419, 39, 604), (0.17, 346, 401, 40, 622), (0.18, 344, 384, 42, 639), (0.19, 338, 369, 48, 654), (0.2, 333, 356, 53, 667), (0.21, 329, 341, 57, 682), (0.22, 323, 322, 63, 701), (0.23, 320, 313, 66, 710), (0.24, 316, 304, 70, 719), (0.25, 309, 291, 77, 732), (0.26, 304, 281, 82, 742), (0.27, 303, 270, 83, 753), (0.28, 295, 256, 91, 767), (0.29, 291, 244, 95, 779), (0.3, 284, 236, 102, 787), (0.31, 280, 230, 106, 793), (0.32, 278, 225, 108, 798), (0.33, 276, 221, 110, 802), (0.34, 274, 212, 112, 811), (0.35000000000000003, 272, 207, 114, 816), (0.36, 267, 201, 119, 822), (0.37, 265, 197, 121, 826), (0.38, 260, 185, 126, 838), (0.39, 253, 179, 133, 844), (0.4, 249, 166, 137, 857), (0.41000000000000003, 246, 159, 140, 864), (0.42, 243, 158, 143, 865), (0.43, 241, 150, 145, 873), (0.44, 234, 147, 152, 876), (0.45, 230, 135, 156, 888), (0.46, 224, 125, 162, 898), (0.47000000000000003, 218, 120, 168, 903), (0.48, 217, 115, 169, 908), (0.49, 213, 110, 173, 913), (0.5, 210, 101, 176, 922), (0.51, 207, 99, 179, 924), (0.52, 204, 93, 182, 930), (0.53, 196, 91, 190, 932), (0.54, 194, 86, 192, 937), (0.55, 185, 79, 201, 944), (0.56, 182, 76, 204, 947), (0.5700000000000001, 176, 68, 210, 955), (0.58, 171, 61, 215, 962), (0.59, 163, 59, 223, 964), (0.6, 151, 53, 235, 970), (0.61, 145, 49, 241, 974), (0.62, 141, 46, 245, 977), (0.63, 133, 40, 253, 983), (0.64, 125, 37, 261, 986), (0.65, 119, 34, 267, 989), (0.66, 114, 31, 272, 992), (0.67, 105, 29, 281, 994), (0.68, 94, 26, 292, 997), (0.6900000000000001, 88, 25, 298, 998), (0.7000000000000001, 76, 20, 310, 1003), (0.71, 63, 14, 323, 1009), (0.72, 57, 11, 329, 1012), (0.73, 47, 10, 339, 1013), (0.74, 41, 8, 345, 1015), (0.75, 33, 7, 353, 1016), (0.76, 30, 6, 356, 1017), (0.77, 25, 5, 361, 1018), (0.78, 19, 3, 367, 1020), (0.79, 15, 2, 371, 1021), (0.8, 13, 2, 373, 1021), (0.81, 6, 0, 380, 1023), (0.8200000000000001, 5, 0, 381, 1023), (0.8300000000000001, 3, 0, 383, 1023), (0.84, 0, 0, 386, 1023), (0.85, 0, 0, 386, 1023), (0.86, 0, 0, 386, 1023), (0.87, 0, 0, 386, 1023), (0.88, 0, 0, 386, 1023), (0.89, 0, 0, 386, 1023), (0.9, 0, 0, 386, 1023), (0.91, 0, 0, 386, 1023), (0.92, 0, 0, 386, 1023), (0.93, 0, 0, 386, 1023), (0.9400000000000001, 0, 0, 386, 1023), (0.9500000000000001, 0, 0, 386, 1023), (0.96, 0, 0, 386, 1023), (0.97, 0, 0, 386, 1023), (0.98, 0, 0, 386, 1023), (0.99, 0, 0, 386, 1023), (1.0, 0, 0, 386, 1023)]
df_scores = pd.DataFrame(scores)
df_scores
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0.00 | 386 | 1023 | 0 | 0 |
| 1 | 0.01 | 385 | 914 | 1 | 109 |
| 2 | 0.02 | 384 | 830 | 2 | 193 |
| 3 | 0.03 | 383 | 766 | 3 | 257 |
| 4 | 0.04 | 381 | 715 | 5 | 308 |
| … | … | … | … | … | … |
| 96 | 0.96 | 0 | 0 | 386 | 1023 |
| 97 | 0.97 | 0 | 0 | 386 | 1023 |
| 98 | 0.98 | 0 | 0 | 386 | 1023 |
| 99 | 0.99 | 0 | 0 | 386 | 1023 |
| 100 | 1.00 | 0 | 0 | 386 | 1023 |
101 rows × 5 columns
columns = ['threshold', 'tp', 'fp', 'fn', 'tn']
df_scores = pd.DataFrame(scores, columns = columns)
df_scores[::10] # looking at each 10th record
| threshold | tp | fp | fn | tn | |
|---|---|---|---|---|---|
| 0 | 0.0 | 386 | 1023 | 0 | 0 |
| 10 | 0.1 | 366 | 556 | 20 | 467 |
| 20 | 0.2 | 333 | 356 | 53 | 667 |
| 30 | 0.3 | 284 | 236 | 102 | 787 |
| 40 | 0.4 | 249 | 166 | 137 | 857 |
| 50 | 0.5 | 210 | 101 | 176 | 922 |
| 60 | 0.6 | 151 | 53 | 235 | 970 |
| 70 | 0.7 | 76 | 20 | 310 | 1003 |
| 80 | 0.8 | 13 | 2 | 373 | 1021 |
| 90 | 0.9 | 0 | 0 | 386 | 1023 |
| 100 | 1.0 | 0 | 0 | 386 | 1023 |
df_scores['tpr'] = df_scores.tp / (df_scores.tp + df_scores.fn)
df_scores['fpr'] = df_scores.fp / (df_scores.fp + df_scores.tn)
df_scores[::10]
| threshold | tp | fp | fn | tn | tpr | fpr | |
|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 386 | 1023 | 0 | 0 | 1.000000 | 1.000000 |
| 10 | 0.1 | 366 | 556 | 20 | 467 | 0.948187 | 0.543500 |
| 20 | 0.2 | 333 | 356 | 53 | 667 | 0.862694 | 0.347996 |
| 30 | 0.3 | 284 | 236 | 102 | 787 | 0.735751 | 0.230694 |
| 40 | 0.4 | 249 | 166 | 137 | 857 | 0.645078 | 0.162268 |
| 50 | 0.5 | 210 | 101 | 176 | 922 | 0.544041 | 0.098729 |
| 60 | 0.6 | 151 | 53 | 235 | 970 | 0.391192 | 0.051808 |
| 70 | 0.7 | 76 | 20 | 310 | 1003 | 0.196891 | 0.019550 |
| 80 | 0.8 | 13 | 2 | 373 | 1021 | 0.033679 | 0.001955 |
| 90 | 0.9 | 0 | 0 | 386 | 1023 | 0.000000 | 0.000000 |
| 100 | 1.0 | 0 | 0 | 386 | 1023 | 0.000000 | 0.000000 |
plt.plot(df_scores.threshold, df_scores['tpr'], label='TPR')
plt.plot(df_scores.threshold, df_scores['fpr'], label='FPR')
plt.xlabel('Threshold')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x2930d5ff880>
Random model¶
np.random.seed(1)
y_rand = np.random.uniform(0, 1, size=len(y_val))
y_rand.round(3)
array([0.417, 0.72 , 0. , ..., 0.774, 0.334, 0.089])
((y_rand >= 0.5) == y_val).mean()
0.5017743080198722
def tpr_fpr_dataframe(y_val, y_pred):
scores = []
thresholds = np.linspace(0, 1, 101)
for t in thresholds:
actual_positive = (y_val == 1)
actual_negative = (y_val == 0)
predict_positive = (y_pred >= t)
predict_negative = (y_pred < t)
tp = (predict_positive & actual_positive).sum()
tn = (predict_negative & actual_negative).sum()
fp = (predict_positive & actual_negative).sum()
fn = (predict_negative & actual_positive).sum()
scores.append((t, tp, fp, fn, tn))
columns = ['threshold', 'tp', 'fp', 'fn', 'tn']
df_scores = pd.DataFrame(scores, columns = columns)
df_scores['tpr'] = df_scores.tp / (df_scores.tp + df_scores.fn)
df_scores['fpr'] = df_scores.fp / (df_scores.fp + df_scores.tn)
return df_scores
df_rand = tpr_fpr_dataframe(y_val, y_rand)
df_rand[::10]
plt.plot(df_rand.threshold, df_rand['tpr'], label='TPR')
plt.plot(df_rand.threshold, df_rand['fpr'], label='FPR')
plt.xlabel('Threshold')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x2930d5e7640>
Ideal model¶
num_neg = (y_val == 0).sum()
num_pos = (y_val == 1).sum()
num_neg, num_pos
(1023, 386)
The np.repeat function will create an array with 0’s the number of times of num_neg and 1’s the number of times of num_pos. This creates the order in the second set in the image.
y_ideal = np.repeat([0, 1], [num_neg, num_pos])
y_ideal
array([0, 0, 0, ..., 1, 1, 1])
y_ideal_pred = np.linspace(0, 1, len(y_val))
1 - y_val.mean()
0.7260468417317246
((y_ideal_pred >= 0.726) == y_ideal).mean()
1.0
df_ideal = tpr_fpr_dataframe(y_ideal, y_ideal_pred)
plt.plot(df_ideal.threshold, df_ideal['tpr'], label='TPR')
plt.plot(df_ideal.threshold, df_ideal['fpr'], label='FPR')
plt.xlabel('Threshold')
plt.ylabel('Accuracy')
plt.legend()
<matplotlib.legend.Legend at 0x2930bcdddb0>
Putting it all together¶
plt.plot(df_scores.threshold, df_scores['tpr'], label='TPR_scores')
plt.plot(df_scores.threshold, df_scores['fpr'], label='FPR_scores')
plt.plot(df_ideal.threshold, df_ideal['tpr'], label='TPR_ideal')
plt.plot(df_ideal.threshold, df_ideal['fpr'], label='FPR_ideal')
#plt.plot(df_rand.threshold, df_rand['tpr'], label='TPR_rand')
#plt.plot(df_rand.threshold, df_rand['fpr'], label='FPR_rand')
plt.legend()
<matplotlib.legend.Legend at 0x293090417b0>
plt.figure(figsize=(5, 5))
plt.plot(df_scores.fpr, df_scores.tpr, label='Model')
#plt.plot(df_rand.fpr, df_rand.tpr, label='random')
#plt.plot(df_ideal.fpr, df_ideal.tpr, label='ideal')
plt.plot([0, 1], [0, 1], label='Random', linestyle='--')
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.legend()
<matplotlib.legend.Legend at 0x2930bf91240>
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_val, y_pred)
plt.figure(figsize=(5, 5))
plt.plot(fpr, tpr, label='Model')
plt.plot([0, 1], [0, 1], label='Random', linestyle='--')
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.legend()
<matplotlib.legend.Legend at 0x2930e905ae0>
4.6 ROC AUC¶
The Area under the ROC curves can tell us how good is our model with a single value. The AUROC of a random model is 0.5, while for an ideal one is 1.
In ther words, AUC can be interpreted as the probability that a randomly selected positive example has a greater score than a randomly selected negative example.
Classes and methods:
auc(x, y)– sklearn.metrics class for calculating area under the curve of the x and y datasets. For ROC curves x would be false positive rate, and y true positive rate.roc_auc_score(x, y)– sklearn.metrics class for calculating area under the ROC curves of the x false positive rate and y true positive rate datasets.
from sklearn.metrics import auc
auc(fpr, tpr)
0.8438302463039216
auc(df_scores.fpr, df_scores.tpr)
0.8438365773732646
auc(df_ideal.fpr, df_ideal.tpr)
0.9999430203759136
fpr, tpr, thresholds = roc_curve(y_val, y_pred)
auc(fpr, tpr)
0.8438302463039216
from sklearn.metrics import roc_auc_score
roc_auc_score(y_val, y_pred)
0.8438302463039216
neg = y_pred[y_val == 0]
pos = y_pred[y_val == 1]
neg
array([0.00899416, 0.20483208, 0.21257239, ..., 0.10764076, 0.31400436,
0.13641188])
import random
Below is an example of how roc_auc_score is actually calculated
n = 1000000
success = 0
for i in range(n):
pos_ind = random.randint(0, len(pos) - 1)
neg_ind = random.randint(0, len(neg) - 1)
if pos[pos_ind] > neg[neg_ind]:
success = success + 1
success / n
0.843749
We can also do this with Numpy
n = 1000000
random.seed(1)
pos_ind = np.random.randint(0, len(pos), size=n)
neg_ind = np.random.randint(0, len(neg), size=n)
(pos[pos_ind] > neg[neg_ind]).mean()
0.843908
4.7 Cross-Validation¶
Extra resources In the lesson we talked about iterators and generators in Python. You can read more about them here:
- https://anandology.com/python-practice-book/iterators.html
- https://www.google.com/search?q=python+iterators+and+generators
Notes
Cross-validation refers to evaluating the same model on different subsets of a dataset, getting the average prediction, and spread within predictions. This method is applied in the parameter tuning step, which is the process of selecting the best parameter.
In this algorithm, the full training dataset is divided into k partitions, we train the model in k-1 partiions of this dataset and evaluate it on the remaining subset. Then, we end up evaluating the model in all the k folds, and we calculate the average evaluation metric for all the folds.
In general, if the dataset is large, we should use the hold-out validation dataset strategy. In the other hand, if the dataset is small or we want to know the standard deviation of the model across different folds, we can use the cross-validation approach.
Libraries, classes and methods:
Kfold(k, s, x)– sklearn.model_selection class for calculating the cross validation with k folds, s boolean attribute for shuffle decision, and an x random stateKfold.split(x)– sklearn.Kfold method for splitting the x dataset with the attributes established in the Kfold’s object construction.for i in tqdm()– library for showing the progress of each i iteration in a for loop.
def train(df_train, y_train, C=1.0):
dicts = df_train[categorical + numerical].to_dict(orient='records')
dv = DictVectorizer(sparse=False)
X_train = dv.fit_transform(dicts)
model = LogisticRegression(C=C, max_iter=1000)
model.fit(X_train, y_train)
return dv, model
dv, model = train(df_train, y_train, C=0.001)
def predict(df, dv, model):
dicts = df[categorical + numerical].to_dict(orient='records')
X = dv.transform(dicts)
y_pred = model.predict_proba(X)[:, 1]
return y_pred
y_pred = predict(df_val, dv, model)
from sklearn.model_selection import KFold
kfold = KFold(n_splits=10, shuffle=True, random_state=1)
train_idx, val_idx = next(kfold.split(df_full_train))
tqdm is a package that allows us to see progress bars during iteration functions.
import sys
!conda install --yes --prefix {sys.prefix} tqdm
Collecting package metadata (current_repodata.json): ...working... done
Solving environment: ...working... done
## Package Plan ##
environment location: C:\Users\daver\Desktop\DataScience\zoomcamp\env
added / updated specs:
- tqdm
The following packages will be downloaded:
package | build
---------------------------|-----------------
certifi-2022.9.14 | py310haa95532_0 155 KB
tqdm-4.64.0 | py310haa95532_0 156 KB
------------------------------------------------------------
Total: 312 KB
The following NEW packages will be INSTALLED:
tqdm pkgs/main/win-64::tqdm-4.64.0-py310haa95532_0
The following packages will be SUPERSEDED by a higher-priority channel:
ca-certificates conda-forge::ca-certificates-2022.9.1~ --> pkgs/main::ca-certificates-2022.07.19-haa95532_0
certifi conda-forge/noarch::certifi-2022.9.14~ --> pkgs/main/win-64::certifi-2022.9.14-py310haa95532_0
openssl conda-forge::openssl-1.1.1q-h8ffe710_0 --> pkgs/main::openssl-1.1.1q-h2bbff1b_0
Downloading and Extracting Packages
tqdm-4.64.0 | 156 KB | | 0%
tqdm-4.64.0 | 156 KB | # | 10%
tqdm-4.64.0 | 156 KB | ### | 31%
tqdm-4.64.0 | 156 KB | #####1 | 51%
tqdm-4.64.0 | 156 KB | ########## | 100%
certifi-2022.9.14 | 155 KB | | 0%
certifi-2022.9.14 | 155 KB | # | 10%
certifi-2022.9.14 | 155 KB | ## | 21%
certifi-2022.9.14 | 155 KB | ####1 | 41%
certifi-2022.9.14 | 155 KB | ########## | 100%
Preparing transaction: ...working... done
Verifying transaction: ...working... done
Executing transaction: ...working... done
Retrieving notices: ...working... done
==> WARNING: A newer version of conda exists. <==
current version: 4.14.0
latest version: 22.9.0
Please update conda by running
$ conda update -n base -c defaults conda
from tqdm.auto import tqdm
n_splits = 5
for C in tqdm([0.001, 0.01, 0.1, 0.5, 1, 5, 10]):
kfold = KFold(n_splits=n_splits, shuffle=True, random_state=1)
scores = []
for train_idx, val_idx in kfold.split(df_full_train):
df_train = df_full_train.iloc[train_idx]
df_val = df_full_train.iloc[val_idx]
y_train = df_train.churn.values
y_val = df_val.churn.values
dv, model = train(df_train, y_train, C=C)
y_pred = predict(df_val, dv, model)
auc = roc_auc_score(y_val, y_pred)
scores.append(auc)
print('C=%s %.3f +- %.3f' % (C, np.mean(scores), np.std(scores)))
0%| | 0/7 [00:00<?, ?it/s]
C=0.001 0.825 +- 0.009 C=0.01 0.840 +- 0.009 C=0.1 0.841 +- 0.008 C=0.5 0.841 +- 0.007 C=1 0.841 +- 0.008 C=5 0.840 +- 0.008 C=10 0.841 +- 0.007
Above we see the scores and they are all very similar, 0.001 is the lowest. All the rest are very close and since C=1.0 is the default we will just use that. Since all the scores were very similar we can run the model on the test data set.
dv, model = train(df_full_train, df_full_train.churn.values, C=1.0)
y_pred = predict(df_test, dv, model)
auc = roc_auc_score(y_test, y_pred)
auc
0.8572386167896259
4.8 Summary¶
General definitions:
- Metric: A single number that describes the performance of a model
- Accuracy: Fraction of correct answers; sometimes misleading
- Precision and recall are less misleading when we have class inbalance
- ROC Curve: A way to evaluate the performance at all thresholds; okay to use with imbalance
- K-Fold CV: More reliable estimate for performance (mean + std)
In brief, this weeks was about different metrics to evaluate a binary classifier. These measures included accuracy, confusion table, precision, recall, ROC curves(TPR, FRP, random model, and ideal model), and AUROC. Also, we talked about a different way to estimate the performance of the model and make the parameter tuning with cross-validation.
4.9 Explore more¶
- Check the precision and recall of the dummy classifier that always predict “FALSE”
- F1 score = 2 P R / (P + R)
- Evaluate precision and recall at different thresholds, plot P vs R – this way you’ll get the precision/recall curve (similar to ROC curve)
- Area under the PR curve is also a useful metric
Other projects
- Calculate the metrics for the suggested datasets from the previous week
Leave a Reply