2. Machine Learning for Regression¶
- 2.1 Car price prediction project
- 2.2 Data preparation
- 2.3 Exploratory data analysis
- 2.4 Setting up the validation framework
- 2.5 Linear regression
- 2.6 Linear regression: vector form
- 2.7 Training linear regression: Normal equation
- 2.8 Baseline model for car price prediction project
- 2.9 Root mean squared error
- 2.10 Using RMSE on validation data
- 2.11 Feature engineering
- 2.12 Categorical variables
- 2.13 Regularization
- 2.14 Tuning the model
- 2.15 Using the model
- 2.16 Car price prediction project summary
2.1 Car price prediction project¶
Project plan:
- Prepare data and Exploratory data analysis (EDA)
- Use linear regression for predicting price
- Understanding the internals of linear regression
- Evaluating the model with RMSE
- Feature engineering
- Regularization
- Using the model
First we import the libraries for manipulating data. Pandas is a python package used to analyze and manipulate data. NumPy is a python package used to work with arrays.
import pandas as pd
import numpy as np
2.2 Data preparation¶
Pandas attributes and methods:
pd.read.csv()– read csv filesdf.head()– take a look of the dataframedf.columns– retrieve colum names of a dataframedf.columns.str.lower()– lowercase all the lettersdf.columns.str.replace(' ', '_')– replace the space separatordf.dtypes– retrieve data types of all featuresdf.index– retrieve indices of a dataframe
data = 'https://raw.githubusercontent.com/alexeygrigorev/mlbookcamp-code/master/chapter-02-car-price/data.csv'
Using wget to download the data needed for this regression
import urllib.request
url = 'https://raw.githubusercontent.com/alexeygrigorev/mlbookcamp-code/master/chapter-02-car-price/data.csv'
filename = 'data.csv'
urllib.request.urlretrieve(url, filename)
('data.csv', <http.client.HTTPMessage at 0x16e163eb730>)
Load the file using pandas read read_csvfunction
df = pd.read_csv('data.csv')
df
| Make | Model | Year | Engine Fuel Type | Engine HP | Engine Cylinders | Transmission Type | Driven_Wheels | Number of Doors | Market Category | Vehicle Size | Vehicle Style | highway MPG | city mpg | Popularity | MSRP | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | BMW | 1 Series M | 2011 | premium unleaded (required) | 335.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Factory Tuner,Luxury,High-Performance | Compact | Coupe | 26 | 19 | 3916 | 46135 |
| 1 | BMW | 1 Series | 2011 | premium unleaded (required) | 300.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Luxury,Performance | Compact | Convertible | 28 | 19 | 3916 | 40650 |
| 2 | BMW | 1 Series | 2011 | premium unleaded (required) | 300.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Luxury,High-Performance | Compact | Coupe | 28 | 20 | 3916 | 36350 |
| 3 | BMW | 1 Series | 2011 | premium unleaded (required) | 230.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Luxury,Performance | Compact | Coupe | 28 | 18 | 3916 | 29450 |
| 4 | BMW | 1 Series | 2011 | premium unleaded (required) | 230.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Luxury | Compact | Convertible | 28 | 18 | 3916 | 34500 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 11909 | Acura | ZDX | 2012 | premium unleaded (required) | 300.0 | 6.0 | AUTOMATIC | all wheel drive | 4.0 | Crossover,Hatchback,Luxury | Midsize | 4dr Hatchback | 23 | 16 | 204 | 46120 |
| 11910 | Acura | ZDX | 2012 | premium unleaded (required) | 300.0 | 6.0 | AUTOMATIC | all wheel drive | 4.0 | Crossover,Hatchback,Luxury | Midsize | 4dr Hatchback | 23 | 16 | 204 | 56670 |
| 11911 | Acura | ZDX | 2012 | premium unleaded (required) | 300.0 | 6.0 | AUTOMATIC | all wheel drive | 4.0 | Crossover,Hatchback,Luxury | Midsize | 4dr Hatchback | 23 | 16 | 204 | 50620 |
| 11912 | Acura | ZDX | 2013 | premium unleaded (recommended) | 300.0 | 6.0 | AUTOMATIC | all wheel drive | 4.0 | Crossover,Hatchback,Luxury | Midsize | 4dr Hatchback | 23 | 16 | 204 | 50920 |
| 11913 | Lincoln | Zephyr | 2006 | regular unleaded | 221.0 | 6.0 | AUTOMATIC | front wheel drive | 4.0 | Luxury | Midsize | Sedan | 26 | 17 | 61 | 28995 |
11914 rows × 16 columns
df.columns is part of the Pandas library that will return the column names of the dataframe.
df.columns
Index(['Make', 'Model', 'Year', 'Engine Fuel Type', 'Engine HP',
'Engine Cylinders', 'Transmission Type', 'Driven_Wheels',
'Number of Doors', 'Market Category', 'Vehicle Size', 'Vehicle Style',
'highway MPG', 'city mpg', 'Popularity', 'MSRP'],
dtype='object')
We want to clean up our column names to remove caps and replace spaces with underscores and the operations can be chained together and reassigned to the columns variable. The str.lower() is a method for altering the selected string to all lower case. The str.replace() method can be used to replace specific characters in the string, in this case we want to replace spaces in column names with an underscore so that we can use dot methods. Dot methods will not work on strings with spaces.
df.columns = df.columns.str.lower().str.replace(' ', '_')
Now when we view the dataframe we can see that the column names no longer contain spaces and everything is lower case.
df
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | BMW | 1 Series M | 2011 | premium unleaded (required) | 335.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Factory Tuner,Luxury,High-Performance | Compact | Coupe | 26 | 19 | 3916 | 46135 |
| 1 | BMW | 1 Series | 2011 | premium unleaded (required) | 300.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Luxury,Performance | Compact | Convertible | 28 | 19 | 3916 | 40650 |
| 2 | BMW | 1 Series | 2011 | premium unleaded (required) | 300.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Luxury,High-Performance | Compact | Coupe | 28 | 20 | 3916 | 36350 |
| 3 | BMW | 1 Series | 2011 | premium unleaded (required) | 230.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Luxury,Performance | Compact | Coupe | 28 | 18 | 3916 | 29450 |
| 4 | BMW | 1 Series | 2011 | premium unleaded (required) | 230.0 | 6.0 | MANUAL | rear wheel drive | 2.0 | Luxury | Compact | Convertible | 28 | 18 | 3916 | 34500 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 11909 | Acura | ZDX | 2012 | premium unleaded (required) | 300.0 | 6.0 | AUTOMATIC | all wheel drive | 4.0 | Crossover,Hatchback,Luxury | Midsize | 4dr Hatchback | 23 | 16 | 204 | 46120 |
| 11910 | Acura | ZDX | 2012 | premium unleaded (required) | 300.0 | 6.0 | AUTOMATIC | all wheel drive | 4.0 | Crossover,Hatchback,Luxury | Midsize | 4dr Hatchback | 23 | 16 | 204 | 56670 |
| 11911 | Acura | ZDX | 2012 | premium unleaded (required) | 300.0 | 6.0 | AUTOMATIC | all wheel drive | 4.0 | Crossover,Hatchback,Luxury | Midsize | 4dr Hatchback | 23 | 16 | 204 | 50620 |
| 11912 | Acura | ZDX | 2013 | premium unleaded (recommended) | 300.0 | 6.0 | AUTOMATIC | all wheel drive | 4.0 | Crossover,Hatchback,Luxury | Midsize | 4dr Hatchback | 23 | 16 | 204 | 50920 |
| 11913 | Lincoln | Zephyr | 2006 | regular unleaded | 221.0 | 6.0 | AUTOMATIC | front wheel drive | 4.0 | Luxury | Midsize | Sedan | 26 | 17 | 61 | 28995 |
11914 rows × 16 columns
The df.dytpes shows us what type of data is contained in each column. We are particularlly interested in the “object” columns as they contain data in a string format.
df.dtypes
make object model object year int64 engine_fuel_type object engine_hp float64 engine_cylinders float64 transmission_type object driven_wheels object number_of_doors float64 market_category object vehicle_size object vehicle_style object highway_mpg int64 city_mpg int64 popularity int64 msrp int64 dtype: object
We can see in the dataframe that the data is also inconsistant in its formatting. Lets clean that up and we start by identifying which columns contain a string format, which is equated by the data type object
df.dtypes == 'object'
make True model True year False engine_fuel_type True engine_hp False engine_cylinders False transmission_type True driven_wheels True number_of_doors False market_category True vehicle_size True vehicle_style True highway_mpg False city_mpg False popularity False msrp False dtype: bool
Now we want to select only those columns (or ‘features’) that are of the data type ‘object’
df.dtypes[df.dtypes == 'object']
make object model object engine_fuel_type object transmission_type object driven_wheels object market_category object vehicle_size object vehicle_style object dtype: object
Now that we know which features are objects we don’t need the return showing us the data types and we can ‘unselect’ those by using .index to just retrieve the index
df.dtypes[df.dtypes == 'object'].index
Index(['make', 'model', 'engine_fuel_type', 'transmission_type',
'driven_wheels', 'market_category', 'vehicle_size', 'vehicle_style'],
dtype='object')
Lets transform those “object” containing column names to a python list and and assign the list to the variable named “strings”.
strings = list(df.dtypes[df.dtypes == 'object'].index)
Now we can create a short function that will iterate through each column in the variable list named “strings” and apply the .lower abd .replace methods to data contained within the column. After we call the df again we can see that all the ‘object’ data with in the dataframe has been transformed to remove spaces and remove all capitlization.
for col in strings:
df[col] = df[col].str.lower().str.replace(' ', '_')
df.head()
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | bmw | 1_series_m | 2011 | premium_unleaded_(required) | 335.0 | 6.0 | manual | rear_wheel_drive | 2.0 | factory_tuner,luxury,high-performance | compact | coupe | 26 | 19 | 3916 | 46135 |
| 1 | bmw | 1_series | 2011 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | convertible | 28 | 19 | 3916 | 40650 |
| 2 | bmw | 1_series | 2011 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,high-performance | compact | coupe | 28 | 20 | 3916 | 36350 |
| 3 | bmw | 1_series | 2011 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | coupe | 28 | 18 | 3916 | 29450 |
| 4 | bmw | 1_series | 2011 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury | compact | convertible | 28 | 18 | 3916 | 34500 |
2.3 Exploratory data analysis¶
Pandas attributes and methods:
df[col].unique()– returns a list of unique values in the seriesdf[col].nunique()– returns the number of unique values in the seriesdf.isnull().sum()– retunrs the number of null values in the dataframe
Matplotlib and seaborn methods:
%matplotlib inline– assure that plots are displayed in jupyter notebook’s cellssns.histplot()– show the histogram of a series
Numpy methods:
np.log1p()– applies log transformation to a variable and adds one to each result
Long-tail distributions usually confuse the ML models, so the recommendation is to transform the target variable distribution to a normal one whenever possible.
df
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | bmw | 1_series_m | 2011 | premium_unleaded_(required) | 335.0 | 6.0 | manual | rear_wheel_drive | 2.0 | factory_tuner,luxury,high-performance | compact | coupe | 26 | 19 | 3916 | 46135 |
| 1 | bmw | 1_series | 2011 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | convertible | 28 | 19 | 3916 | 40650 |
| 2 | bmw | 1_series | 2011 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,high-performance | compact | coupe | 28 | 20 | 3916 | 36350 |
| 3 | bmw | 1_series | 2011 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | coupe | 28 | 18 | 3916 | 29450 |
| 4 | bmw | 1_series | 2011 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury | compact | convertible | 28 | 18 | 3916 | 34500 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 11909 | acura | zdx | 2012 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | all_wheel_drive | 4.0 | crossover,hatchback,luxury | midsize | 4dr_hatchback | 23 | 16 | 204 | 46120 |
| 11910 | acura | zdx | 2012 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | all_wheel_drive | 4.0 | crossover,hatchback,luxury | midsize | 4dr_hatchback | 23 | 16 | 204 | 56670 |
| 11911 | acura | zdx | 2012 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | all_wheel_drive | 4.0 | crossover,hatchback,luxury | midsize | 4dr_hatchback | 23 | 16 | 204 | 50620 |
| 11912 | acura | zdx | 2013 | premium_unleaded_(recommended) | 300.0 | 6.0 | automatic | all_wheel_drive | 4.0 | crossover,hatchback,luxury | midsize | 4dr_hatchback | 23 | 16 | 204 | 50920 |
| 11913 | lincoln | zephyr | 2006 | regular_unleaded | 221.0 | 6.0 | automatic | front_wheel_drive | 4.0 | luxury | midsize | sedan | 26 | 17 | 61 | 28995 |
11914 rows × 16 columns
df.columns
Index(['make', 'model', 'year', 'engine_fuel_type', 'engine_hp',
'engine_cylinders', 'transmission_type', 'driven_wheels',
'number_of_doors', 'market_category', 'vehicle_size', 'vehicle_style',
'highway_mpg', 'city_mpg', 'popularity', 'msrp'],
dtype='object')
We want to learn more about the data that we are using. We can use some simple functions to more fully understand what the data contains.
for col in df.columns:
print(col)
print(df[col].head())
print()
make 0 bmw 1 bmw 2 bmw 3 bmw 4 bmw Name: make, dtype: object model 0 1_series_m 1 1_series 2 1_series 3 1_series 4 1_series Name: model, dtype: object year 0 2011 1 2011 2 2011 3 2011 4 2011 Name: year, dtype: int64 engine_fuel_type 0 premium_unleaded_(required) 1 premium_unleaded_(required) 2 premium_unleaded_(required) 3 premium_unleaded_(required) 4 premium_unleaded_(required) Name: engine_fuel_type, dtype: object engine_hp 0 335.0 1 300.0 2 300.0 3 230.0 4 230.0 Name: engine_hp, dtype: float64 engine_cylinders 0 6.0 1 6.0 2 6.0 3 6.0 4 6.0 Name: engine_cylinders, dtype: float64 transmission_type 0 manual 1 manual 2 manual 3 manual 4 manual Name: transmission_type, dtype: object driven_wheels 0 rear_wheel_drive 1 rear_wheel_drive 2 rear_wheel_drive 3 rear_wheel_drive 4 rear_wheel_drive Name: driven_wheels, dtype: object number_of_doors 0 2.0 1 2.0 2 2.0 3 2.0 4 2.0 Name: number_of_doors, dtype: float64 market_category 0 factory_tuner,luxury,high-performance 1 luxury,performance 2 luxury,high-performance 3 luxury,performance 4 luxury Name: market_category, dtype: object vehicle_size 0 compact 1 compact 2 compact 3 compact 4 compact Name: vehicle_size, dtype: object vehicle_style 0 coupe 1 convertible 2 coupe 3 coupe 4 convertible Name: vehicle_style, dtype: object highway_mpg 0 26 1 28 2 28 3 28 4 28 Name: highway_mpg, dtype: int64 city_mpg 0 19 1 19 2 20 3 18 4 18 Name: city_mpg, dtype: int64 popularity 0 3916 1 3916 2 3916 3 3916 4 3916 Name: popularity, dtype: int64 msrp 0 46135 1 40650 2 36350 3 29450 4 34500 Name: msrp, dtype: int64
The above doesn’t give us much detail, for instance, under ‘make’ it shows all bmw’s but we can use the unique and nunique functions to get a little better understanding of what our data contains. This function will show us the first five unique items in each column and count the number of unique items in each column. For instance we can see there are 48 different manufacturers of cars in the dataset.
for col in df.columns:
print(col) # prints the col name
print(df[col].unique()[:5]) # prints the first 5 unique values in the col
print(df[col].nunique()) # calculates the number of unique values in each col
print()
make ['bmw' 'audi' 'fiat' 'mercedes-benz' 'chrysler'] 48 model ['1_series_m' '1_series' '100' '124_spider' '190-class'] 914 year [2011 2012 2013 1992 1993] 28 engine_fuel_type ['premium_unleaded_(required)' 'regular_unleaded' 'premium_unleaded_(recommended)' 'flex-fuel_(unleaded/e85)' 'diesel'] 10 engine_hp [335. 300. 230. 320. 172.] 356 engine_cylinders [ 6. 4. 5. 8. 12.] 9 transmission_type ['manual' 'automatic' 'automated_manual' 'direct_drive' 'unknown'] 5 driven_wheels ['rear_wheel_drive' 'front_wheel_drive' 'all_wheel_drive' 'four_wheel_drive'] 4 number_of_doors [ 2. 4. 3. nan] 3 market_category ['factory_tuner,luxury,high-performance' 'luxury,performance' 'luxury,high-performance' 'luxury' 'performance'] 71 vehicle_size ['compact' 'midsize' 'large'] 3 vehicle_style ['coupe' 'convertible' 'sedan' 'wagon' '4dr_hatchback'] 16 highway_mpg [26 28 27 25 24] 59 city_mpg [19 20 18 17 16] 69 popularity [3916 3105 819 617 1013] 48 msrp [46135 40650 36350 29450 34500] 6049
Let us see what the distribution of prices are, we can use visualization to do this. We will import Matplotlib and Seaborn. Seaborn is a package built on top of the Matplotlib library that allows enhanced visualizations on data. The %matplotlib inline statement is notifying Jupyter Notebook that we will be doing some plotting.
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
sns.histplot(df.msrp)
<AxesSubplot:xlabel='msrp', ylabel='Count'>
It isn’t a very good plot right off the bat, we can increase it’s readability.
sns.histplot(df.msrp, bins=50) # bins allow us to group the data points into, well, bins
<AxesSubplot:xlabel='msrp', ylabel='Count'>
That is a very long tail, with most of the car prices grouped near the zeros and some cars valued up around 2 million. We will filter out some of the high price outliers to, perhaps, get a better representation of the data.
sns.histplot(df.msrp[df.msrp < 100000], bins=50)
<AxesSubplot:xlabel='msrp', ylabel='Count'>
Our data has that very long tail, which will confuse our model. We will have to do something to change this. Changing the prices to a logarithm scale, will group our prices closer. A standard practice in converting a log scale is adding 1 to each data point. This ensures that there are no errors in the event that one of the points is a zero. For now we are doing this just to the plot the data and see that it is more of a normal distribution. Later we will apply this log transformation to the “msrp” column of our dataset.
price_logs = np.log1p(df.msrp)
price_logs
0 10.739349
1 10.612779
2 10.500977
3 10.290483
4 10.448744
...
11909 10.739024
11910 10.945018
11911 10.832122
11912 10.838031
11913 10.274913
Name: msrp, Length: 11914, dtype: float64
Now we have our prices close together, our graph should look better.
sns.histplot(price_logs, bins=50)
<AxesSubplot:xlabel='msrp', ylabel='Count'>
We have eliminated that long tail off to the right and now our data looks more like a normal distribution.
Missing values¶
df.isnull().sum()
make 0 model 0 year 0 engine_fuel_type 3 engine_hp 69 engine_cylinders 30 transmission_type 0 driven_wheels 0 number_of_doors 6 market_category 3742 vehicle_size 0 vehicle_style 0 highway_mpg 0 city_mpg 0 popularity 0 msrp 0 dtype: int64
2.4 Setting up the validation framework¶
In general, the dataset is split into three parts: training, validation, and test. For each partition, we need to obtain feature matrices (X) and y vectors of targets. First, the size of partitions is calculated, records are shuffled to guarantee that values of the three partitions contain non-sequential records of the dataset, and the partitions are created with the shuffled indices.
Pandas attributes and methods:
df.iloc[]– returns subsets of records of a dataframe, being selected by numerical indicesdf.reset_index()– restate the orginal indicesdel df[col]– eliminates target variable
Numpy methods:
np.arange()– returns an array of numbersnp.random.shuffle()– returns a shuffled arraynp.random.seed()– set a seed
Let’s draw it
len(df)
11914
We have 11,914 records that need to be separated into training, validation and testing sets. Lets calculate how many records will be in each set using len() and some math.
n = len(df)
n_val = int(n * 0.2)
n_test = int(n * 0.2)
n_train = n - n_val - n_test
n_train, n_val, n_test
(7150, 2382, 2382)
So our training set will contain 7,150 records, and the validation and test sets will contain 2382 each.
df.iloc[:10] # first 10 records
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | bmw | 1_series_m | 2011 | premium_unleaded_(required) | 335.0 | 6.0 | manual | rear_wheel_drive | 2.0 | factory_tuner,luxury,high-performance | compact | coupe | 26 | 19 | 3916 | 46135 |
| 1 | bmw | 1_series | 2011 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | convertible | 28 | 19 | 3916 | 40650 |
| 2 | bmw | 1_series | 2011 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,high-performance | compact | coupe | 28 | 20 | 3916 | 36350 |
| 3 | bmw | 1_series | 2011 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | coupe | 28 | 18 | 3916 | 29450 |
| 4 | bmw | 1_series | 2011 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury | compact | convertible | 28 | 18 | 3916 | 34500 |
| 5 | bmw | 1_series | 2012 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | coupe | 28 | 18 | 3916 | 31200 |
| 6 | bmw | 1_series | 2012 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | convertible | 26 | 17 | 3916 | 44100 |
| 7 | bmw | 1_series | 2012 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,high-performance | compact | coupe | 28 | 20 | 3916 | 39300 |
| 8 | bmw | 1_series | 2012 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury | compact | convertible | 28 | 18 | 3916 | 36900 |
| 9 | bmw | 1_series | 2013 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury | compact | convertible | 27 | 18 | 3916 | 37200 |
df.iloc[10:20] # second 10 records
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | bmw | 1_series | 2013 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,high-performance | compact | coupe | 28 | 20 | 3916 | 39600 |
| 11 | bmw | 1_series | 2013 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | coupe | 28 | 19 | 3916 | 31500 |
| 12 | bmw | 1_series | 2013 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | convertible | 28 | 19 | 3916 | 44400 |
| 13 | bmw | 1_series | 2013 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury | compact | convertible | 28 | 19 | 3916 | 37200 |
| 14 | bmw | 1_series | 2013 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | coupe | 28 | 19 | 3916 | 31500 |
| 15 | bmw | 1_series | 2013 | premium_unleaded_(required) | 320.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,high-performance | compact | convertible | 25 | 18 | 3916 | 48250 |
| 16 | bmw | 1_series | 2013 | premium_unleaded_(required) | 320.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,high-performance | compact | coupe | 28 | 20 | 3916 | 43550 |
| 17 | audi | 100 | 1992 | regular_unleaded | 172.0 | 6.0 | manual | front_wheel_drive | 4.0 | luxury | midsize | sedan | 24 | 17 | 3105 | 2000 |
| 18 | audi | 100 | 1992 | regular_unleaded | 172.0 | 6.0 | manual | front_wheel_drive | 4.0 | luxury | midsize | sedan | 24 | 17 | 3105 | 2000 |
| 19 | audi | 100 | 1992 | regular_unleaded | 172.0 | 6.0 | automatic | all_wheel_drive | 4.0 | luxury | midsize | wagon | 20 | 16 | 3105 | 2000 |
df.iloc[11910:] #last 4 records because the dataset has 11,914 records
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11910 | acura | zdx | 2012 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | all_wheel_drive | 4.0 | crossover,hatchback,luxury | midsize | 4dr_hatchback | 23 | 16 | 204 | 56670 |
| 11911 | acura | zdx | 2012 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | all_wheel_drive | 4.0 | crossover,hatchback,luxury | midsize | 4dr_hatchback | 23 | 16 | 204 | 50620 |
| 11912 | acura | zdx | 2013 | premium_unleaded_(recommended) | 300.0 | 6.0 | automatic | all_wheel_drive | 4.0 | crossover,hatchback,luxury | midsize | 4dr_hatchback | 23 | 16 | 204 | 50920 |
| 11913 | lincoln | zephyr | 2006 | regular_unleaded | 221.0 | 6.0 | automatic | front_wheel_drive | 4.0 | luxury | midsize | sedan | 26 | 17 | 61 | 28995 |
Now we could just grab our records using .iloc and the new variables we just set up.
df_train = df.iloc[:n_train]
df_val = df.iloc[n_train:n_train+n_val]
df_test = df.iloc[n_train+n_val:]
The problem with breaking up our records like this will be that it isn’t a cross-section of records. For example, df_train will contain all of the bmw vehicles. So we need to do something to fhuffle the records around.
df_train
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | bmw | 1_series_m | 2011 | premium_unleaded_(required) | 335.0 | 6.0 | manual | rear_wheel_drive | 2.0 | factory_tuner,luxury,high-performance | compact | coupe | 26 | 19 | 3916 | 46135 |
| 1 | bmw | 1_series | 2011 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | convertible | 28 | 19 | 3916 | 40650 |
| 2 | bmw | 1_series | 2011 | premium_unleaded_(required) | 300.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,high-performance | compact | coupe | 28 | 20 | 3916 | 36350 |
| 3 | bmw | 1_series | 2011 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury,performance | compact | coupe | 28 | 18 | 3916 | 29450 |
| 4 | bmw | 1_series | 2011 | premium_unleaded_(required) | 230.0 | 6.0 | manual | rear_wheel_drive | 2.0 | luxury | compact | convertible | 28 | 18 | 3916 | 34500 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 7145 | mazda | navajo | 1994 | regular_unleaded | 160.0 | 6.0 | manual | four_wheel_drive | 2.0 | NaN | compact | 2dr_suv | 18 | 14 | 586 | 2000 |
| 7146 | mazda | navajo | 1994 | regular_unleaded | 160.0 | 6.0 | manual | four_wheel_drive | 2.0 | NaN | compact | 2dr_suv | 18 | 14 | 586 | 2000 |
| 7147 | lincoln | navigator | 2015 | regular_unleaded | 365.0 | 6.0 | automatic | four_wheel_drive | 4.0 | luxury | large | 4dr_suv | 20 | 15 | 61 | 65055 |
| 7148 | lincoln | navigator | 2015 | regular_unleaded | 365.0 | 6.0 | automatic | four_wheel_drive | 4.0 | luxury | large | 4dr_suv | 19 | 15 | 61 | 67220 |
| 7149 | lincoln | navigator | 2015 | regular_unleaded | 365.0 | 6.0 | automatic | rear_wheel_drive | 4.0 | luxury | large | 4dr_suv | 22 | 16 | 61 | 61480 |
7150 rows × 16 columns
We use the np.arange method to sort the dataframe and then assign it to the variable “idx”.
idx = np.arange(n)
idx
array([ 0, 1, 2, ..., 11911, 11912, 11913])
Then we can use .random.shuffle() to shuffle everything around so that all the bmw’s are not in the train test set.
Since I am doing this as part of the ml-zoomcamp class we want us to have the same shuffle for our data that our instructor has. We can do this by using the np.random.seed() method. and then we will do the suffle again.
np.random.seed(2)
np.random.shuffle(idx)
df_train = df.iloc[idx[:n_train]]
df_val = df.iloc[idx[n_train:n_train+n_val]]
df_test = df.iloc[idx[n_train+n_val:]]
df_train.head()
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2735 | chevrolet | cobalt | 2008 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 2.0 | NaN | compact | coupe | 33 | 24 | 1385 | 14410 |
| 6720 | toyota | matrix | 2012 | regular_unleaded | 132.0 | 4.0 | automatic | front_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 32 | 25 | 2031 | 19685 |
| 5878 | subaru | impreza | 2016 | regular_unleaded | 148.0 | 4.0 | automatic | all_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 37 | 28 | 640 | 19795 |
| 11190 | volkswagen | vanagon | 1991 | regular_unleaded | 90.0 | 4.0 | manual | rear_wheel_drive | 3.0 | NaN | large | passenger_minivan | 18 | 16 | 873 | 2000 |
| 4554 | ford | f-150 | 2017 | flex-fuel_(unleaded/e85) | 385.0 | 8.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | crew_cab_pickup | 21 | 15 | 5657 | 56260 |
len(df_train), len(df_val), len(df_val)
(7150, 2382, 2382)
df_train
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | msrp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2735 | chevrolet | cobalt | 2008 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 2.0 | NaN | compact | coupe | 33 | 24 | 1385 | 14410 |
| 6720 | toyota | matrix | 2012 | regular_unleaded | 132.0 | 4.0 | automatic | front_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 32 | 25 | 2031 | 19685 |
| 5878 | subaru | impreza | 2016 | regular_unleaded | 148.0 | 4.0 | automatic | all_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 37 | 28 | 640 | 19795 |
| 11190 | volkswagen | vanagon | 1991 | regular_unleaded | 90.0 | 4.0 | manual | rear_wheel_drive | 3.0 | NaN | large | passenger_minivan | 18 | 16 | 873 | 2000 |
| 4554 | ford | f-150 | 2017 | flex-fuel_(unleaded/e85) | 385.0 | 8.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | crew_cab_pickup | 21 | 15 | 5657 | 56260 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 434 | bmw | 4_series | 2015 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | rear_wheel_drive | 2.0 | luxury,performance | midsize | convertible | 31 | 20 | 3916 | 54900 |
| 1902 | volkswagen | beetle | 2015 | premium_unleaded_(recommended) | 210.0 | 4.0 | automated_manual | front_wheel_drive | 2.0 | hatchback,performance | compact | 2dr_hatchback | 30 | 24 | 873 | 29215 |
| 9334 | gmc | sierra_1500 | 2015 | flex-fuel_(unleaded/e85) | 285.0 | 6.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | extended_cab_pickup | 22 | 17 | 549 | 34675 |
| 5284 | rolls-royce | ghost | 2014 | premium_unleaded_(required) | 563.0 | 12.0 | automatic | rear_wheel_drive | 4.0 | exotic,luxury,performance | large | sedan | 21 | 13 | 86 | 303300 |
| 2420 | volkswagen | cc | 2017 | premium_unleaded_(recommended) | 200.0 | 4.0 | automated_manual | front_wheel_drive | 4.0 | performance | midsize | sedan | 31 | 22 | 873 | 37820 |
7150 rows × 16 columns
Now that we have a randomly shuffled dataframe we want to reset the index so that is in numerical order.
df_train = df_train.reset_index(drop=True)
df_val = df_val.reset_index(drop=True)
df_test = df_test.reset_index(drop=True)
Before we start the regression problem we need to apply the log function to the “msrp” column so that the data doesn’t have that long tail.
df_train.msrp
0 14410
1 19685
2 19795
3 2000
4 56260
...
7145 54900
7146 29215
7147 34675
7148 303300
7149 37820
Name: msrp, Length: 7150, dtype: int64
We will use the np.log1p function to perform this on the data.
np.log1p(df_train.msrp)
0 9.575747
1 9.887663
2 9.893235
3 7.601402
4 10.937757
...
7145 10.913287
7146 10.282472
7147 10.453803
7148 12.622481
7149 10.540620
Name: msrp, Length: 7150, dtype: float64
The data above is a series, we will convert that to a pandas array and then assign it to the “y_train” variable and then we will do that to the other sets as well.
y_train = np.log1p(df_train.msrp.values)
y_val = np.log1p(df_val.msrp.values)
y_test = np.log1p(df_test.msrp.values)
None of our df sets, i.e. df_test, need the msrp column because that is what we are trying to predict. We will delete that column from our df sets.
del df_train['msrp']
del df_val['msrp']
del df_test['msrp']
len(y_train)
7150
2.5 Linear regression¶
Model for solving regression tasks, in which the objective is to adjust a line for the data and make predictions on new values. The input of this model is the feature matrix and a y vector of predictions is obtained, trying to be as close as possible to the actual y values. The LR formula is the sum of the bias term (WO), which refers to the predictions if there is no information, and each of the feature values times their corresponding weights. We need to assure that the result is shown on the untransformed scale.
So our model is g, df_train, df_val and df_test are matricour feature matrices and our targets are the variables we created with y_train, y_val and y_test
df_train
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | chevrolet | cobalt | 2008 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 2.0 | NaN | compact | coupe | 33 | 24 | 1385 |
| 1 | toyota | matrix | 2012 | regular_unleaded | 132.0 | 4.0 | automatic | front_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 32 | 25 | 2031 |
| 2 | subaru | impreza | 2016 | regular_unleaded | 148.0 | 4.0 | automatic | all_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 37 | 28 | 640 |
| 3 | volkswagen | vanagon | 1991 | regular_unleaded | 90.0 | 4.0 | manual | rear_wheel_drive | 3.0 | NaN | large | passenger_minivan | 18 | 16 | 873 |
| 4 | ford | f-150 | 2017 | flex-fuel_(unleaded/e85) | 385.0 | 8.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | crew_cab_pickup | 21 | 15 | 5657 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 7145 | bmw | 4_series | 2015 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | rear_wheel_drive | 2.0 | luxury,performance | midsize | convertible | 31 | 20 | 3916 |
| 7146 | volkswagen | beetle | 2015 | premium_unleaded_(recommended) | 210.0 | 4.0 | automated_manual | front_wheel_drive | 2.0 | hatchback,performance | compact | 2dr_hatchback | 30 | 24 | 873 |
| 7147 | gmc | sierra_1500 | 2015 | flex-fuel_(unleaded/e85) | 285.0 | 6.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | extended_cab_pickup | 22 | 17 | 549 |
| 7148 | rolls-royce | ghost | 2014 | premium_unleaded_(required) | 563.0 | 12.0 | automatic | rear_wheel_drive | 4.0 | exotic,luxury,performance | large | sedan | 21 | 13 | 86 |
| 7149 | volkswagen | cc | 2017 | premium_unleaded_(recommended) | 200.0 | 4.0 | automated_manual | front_wheel_drive | 4.0 | performance | midsize | sedan | 31 | 22 | 873 |
7150 rows × 15 columns
We can look at different records in our dataset, below we are looking at the row indexed at 10 using the .loc[] method.
df_train.iloc[10]
make rolls-royce model phantom_drophead_coupe year 2015 engine_fuel_type premium_unleaded_(required) engine_hp 453.0 engine_cylinders 12.0 transmission_type automatic driven_wheels rear_wheel_drive number_of_doors 2.0 market_category exotic,luxury,performance vehicle_size large vehicle_style convertible highway_mpg 19 city_mpg 11 popularity 86 Name: 10, dtype: object
We are going to choose engine_hp, city_mpg and popularity.
xi = [453, 11, 86]
# this is our feature set for our example
Now we will right a short function to predict a price based on the feature set we chose.
def g(xi):
# do something
return 10000
g(xi)
10000
w0 = 0
w = [1, 1, 1]
Each feature in xi will be assigned a weight to either increase or decrease the efficacy on the price of a vehicle.
With Python we start at 0 so it would be from 0 to 2 for our 3 features.
def linear_regression(xi):
n = len(xi)
pred = w0
for j in range(n):
pred = pred + w[j] * xi[j]
return pred
linear_regression(xi)
550
So our prediction was 550 for the price of the vehicle, in log + 1. It isn’t correct because w0 and w aren’t the correct starting points, that is where machine learning comes in but lets keep working at this solution. Keep in mind the returns we are getting are in a log price that have to back-transform the log. Also, because we did np.log1p() which added a 1, we can use np.expm1 to back-transform and subtract 1.
xi = [453, 11, 86] # features
w0 = 7.17 # bias term
w = [0.01, 0.04, 0.002] # weights
def linear_regression(xi):
n = len(xi)
pred = w0
for j in range(n):
pred = pred + w[j] * xi[j]
return pred
linear_regression(xi)
12.312
Back-transform the log.
np.expm1(linear_regression(xi))
222347.2221101062
The value above is our first attempt and predicting the price of the Rolls-Royce @ 222,347
2.6 Linear regression: vector form¶
The formula of LR can be synthesized with the dot product between features and weights. The feature vector includes the bias term with an x value of one. When all the records are included, the LR can be calculated with the dot product between feature matrix and vector of weights, obtaining the y vector of predictions.
def dot(xi, w):
n = len(xi)
res = 0.0
for j in range(n):
res = res + xi[j] * w[j]
return res
w_new = [w0] + w
w_new
[7.17, 0.01, 0.04, 0.002]
def linear_regression(xi):
xi = [1] + xi
return dot(xi, w_new)
linear_regression(xi)
12.312
Now we will do another prediction on another record (making some numbers up just for the example)
w_new = [w0] + w
w0 = 7.17 # bias term
w = [0.01, 0.04, 0.002] # weights
x1 = [1, 148, 24, 1385]
x2 = [1, 132, 25, 2031]
x10 = [1, 453, 11, 86]
X = [x1, x2, x10]
X = np.array(X)
X
array([[ 1, 148, 24, 1385],
[ 1, 132, 25, 2031],
[ 1, 453, 11, 86]])
def linear_regression(X):
return X.dot(w_new)
linear_regression(X)
array([12.38 , 13.552, 12.312])
2.7 Training linear regression: Normal equation¶
Obtaining predictions as close as possible to y target values requires the calculation of weights from the general LR equation. The feature matrix does not have an inverse because it is not square, so it is required to obtain an approximate solution, which can be obtained using the Gram matrix (multiplication of feature matrix and its transpose). The vector of weights or coefficients obtained with this formula is the closest possible solution to the LR system.
def train_linear_regression(X, y):
pass
X = [[148, 24, 1385],
[132, 25, 2031],
[453, 11, 86],
[158, 24, 185],
[172, 25, 201],
[413, 11, 86],
[38, 54, 185],
[142, 25, 431],
[453, 31, 86]
]
X = np.array(X)
X
array([[ 148, 24, 1385],
[ 132, 25, 2031],
[ 453, 11, 86],
[ 158, 24, 185],
[ 172, 25, 201],
[ 413, 11, 86],
[ 38, 54, 185],
[ 142, 25, 431],
[ 453, 31, 86]])
We need to add our bias terms into the array, which will be 1’s. We will take the shape of the array above and assign the row count to the np.ones method to create a vector of 1’s to match the matrix and then we will append that vector to the matrix
ones = np.ones(X.shape[0])
ones
array([1., 1., 1., 1., 1., 1., 1., 1., 1.])
X = np.column_stack([ones, X])
We need to create a y vector.
y = [100, 200, 150, 250, 100, 200, 150, 250, 120]
XTX = X.T.dot(X) # this is our Gram matrix
XTX
array([[9.000000e+00, 2.109000e+03, 2.300000e+02, 4.676000e+03],
[2.109000e+03, 6.964710e+05, 4.411500e+04, 7.185400e+05],
[2.300000e+02, 4.411500e+04, 7.146000e+03, 1.188030e+05],
[4.676000e+03, 7.185400e+05, 1.188030e+05, 6.359986e+06]])
We now create our inverse matrix, which actuall creates an identity matrix.
XTX_inv = np.linalg.inv(XTX)
We can use the dot product of XTX and XTX_inv to see if we have created an identity matrix, and we have.
XTX.dot(XTX_inv).round(1)
array([[ 1., -0., 0., 0.],
[ 0., 1., 0., -0.],
[ 0., 0., 1., 0.],
[ 0., -0., 0., 1.]])
w_full = XTX_inv.dot(X.T).dot(y)
w_full
array([ 3.00067767e+02, -2.27742529e-01, -2.57694130e+00, -2.30120640e-02])
w0 = w_full[0]
w = w_full[1:]
w0, w
(300.06776692555593, array([-0.22774253, -2.5769413 , -0.02301206]))
def train_linear_regression(X, y):
ones = np.ones(X.shape[0])
X = np.column_stack([ones, X])
XTX = X.T.dot(X)
XTX_inv = np.linalg.inv(XTX)
w_full = XTX_inv.dot(X.T).dot(y)
return w_full[0], w_full[1:]
train_linear_regression(X, y)
(300.06776692555593, array([-0.22774253, -2.5769413 , -0.02301206]))
2.8 Baseline model for car price prediction project¶
The LR model obtained in the previous section was used with the dataset of car price prediction. For this model, only the numerical variables were considered. The training data was pre-processed, replacing the NaN values with 0, in such a way that these values were omitted by the model. Then, the model was trained and it allowed to make predictions on new data. Finally, distributions of y target variable and predictions were compared by plotting their histograms.
df_train
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | chevrolet | cobalt | 2008 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 2.0 | NaN | compact | coupe | 33 | 24 | 1385 |
| 1 | toyota | matrix | 2012 | regular_unleaded | 132.0 | 4.0 | automatic | front_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 32 | 25 | 2031 |
| 2 | subaru | impreza | 2016 | regular_unleaded | 148.0 | 4.0 | automatic | all_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 37 | 28 | 640 |
| 3 | volkswagen | vanagon | 1991 | regular_unleaded | 90.0 | 4.0 | manual | rear_wheel_drive | 3.0 | NaN | large | passenger_minivan | 18 | 16 | 873 |
| 4 | ford | f-150 | 2017 | flex-fuel_(unleaded/e85) | 385.0 | 8.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | crew_cab_pickup | 21 | 15 | 5657 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 7145 | bmw | 4_series | 2015 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | rear_wheel_drive | 2.0 | luxury,performance | midsize | convertible | 31 | 20 | 3916 |
| 7146 | volkswagen | beetle | 2015 | premium_unleaded_(recommended) | 210.0 | 4.0 | automated_manual | front_wheel_drive | 2.0 | hatchback,performance | compact | 2dr_hatchback | 30 | 24 | 873 |
| 7147 | gmc | sierra_1500 | 2015 | flex-fuel_(unleaded/e85) | 285.0 | 6.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | extended_cab_pickup | 22 | 17 | 549 |
| 7148 | rolls-royce | ghost | 2014 | premium_unleaded_(required) | 563.0 | 12.0 | automatic | rear_wheel_drive | 4.0 | exotic,luxury,performance | large | sedan | 21 | 13 | 86 |
| 7149 | volkswagen | cc | 2017 | premium_unleaded_(recommended) | 200.0 | 4.0 | automated_manual | front_wheel_drive | 4.0 | performance | midsize | sedan | 31 | 22 | 873 |
7150 rows × 15 columns
df_train.dtypes
make object model object year int64 engine_fuel_type object engine_hp float64 engine_cylinders float64 transmission_type object driven_wheels object number_of_doors float64 market_category object vehicle_size object vehicle_style object highway_mpg int64 city_mpg int64 popularity int64 dtype: object
We are going to build a model using the features engine_hp, engine_cylinders, highway_mgp, city_mpg, and popularity.
df_train.columns
Index(['make', 'model', 'year', 'engine_fuel_type', 'engine_hp',
'engine_cylinders', 'transmission_type', 'driven_wheels',
'number_of_doors', 'market_category', 'vehicle_size', 'vehicle_style',
'highway_mpg', 'city_mpg', 'popularity'],
dtype='object')
We assign the columns we want to create a model on and assign it to the variable ‘base’.
base = ['engine_hp', 'engine_cylinders', 'highway_mpg',
'city_mpg', 'popularity']
df_train[base]
| engine_hp | engine_cylinders | highway_mpg | city_mpg | popularity | |
|---|---|---|---|---|---|
| 0 | 148.0 | 4.0 | 33 | 24 | 1385 |
| 1 | 132.0 | 4.0 | 32 | 25 | 2031 |
| 2 | 148.0 | 4.0 | 37 | 28 | 640 |
| 3 | 90.0 | 4.0 | 18 | 16 | 873 |
| 4 | 385.0 | 8.0 | 21 | 15 | 5657 |
| … | … | … | … | … | … |
| 7145 | 300.0 | 6.0 | 31 | 20 | 3916 |
| 7146 | 210.0 | 4.0 | 30 | 24 | 873 |
| 7147 | 285.0 | 6.0 | 22 | 17 | 549 |
| 7148 | 563.0 | 12.0 | 21 | 13 | 86 |
| 7149 | 200.0 | 4.0 | 31 | 22 | 873 |
7150 rows × 5 columns
Next, we need to extract the values from our columns to use in our model and we assign those values to the variable ‘X_train’.
X_train = df_train[base].values
X_train
array([[ 148., 4., 33., 24., 1385.],
[ 132., 4., 32., 25., 2031.],
[ 148., 4., 37., 28., 640.],
...,
[ 285., 6., 22., 17., 549.],
[ 563., 12., 21., 13., 86.],
[ 200., 4., 31., 22., 873.]])
We have already created our ‘y’ with the MSRP column that we removed from ‘df_train’ earlier.
y_train
array([ 9.57574708, 9.887663 , 9.89323518, ..., 10.45380308,
12.62248099, 10.54061978])
With the ‘X_train’ and ‘y_train’ variables we can insert these into the train_linear_regression function we created earlier.
train_linear_regression(X_train, y_train)
(nan, array([nan, nan, nan, nan, nan]))
As we can see above we have some ‘nan’ values, which we can’t have. We noticed earlier that we had some null values in the dataset, we have fill those in with some values.
df_train[base].isnull().sum()
engine_hp 40 engine_cylinders 14 highway_mpg 0 city_mpg 0 popularity 0 dtype: int64
As we can see above we have 40 empty entries for ‘engine_hp’ and 14 for ‘engine_cylinders’. There are various ways to fill in these values. We can use the median or mean values of the columns or fill them with a 0.
X_train = df_train[base].fillna(0).values
Now that we have filled in the nan values we can see that our function now works properly.
train_linear_regression(X_train, y_train)
(7.927257388070117,
array([ 9.70589522e-03, -1.59103494e-01, 1.43792133e-02, 1.49441072e-02,
-9.06908672e-06]))
Let’s assign the model to our bias term and w.
w0, w = train_linear_regression(X_train, y_train)
Now we can do the matrix to matrix multiplication to get our predictions.
w0 + X_train.dot(w)
array([ 9.54792783, 9.38733977, 9.67197758, ..., 10.30423015,
11.9778914 , 9.99863111])
Let’s assign our predictions to the variable ‘y_pred’.
y_pred = w0 + X_train.dot(w)
Let’s plot our ‘y_preds’ to see how they comapre to ‘y_train’, which are the actual MSRP’s from our data, which are also known as the target variables. We will can assign different colors for each, the ‘alpha’ argument changes the transparency so that we can see both and the ‘bins’ argument breaks the data into 50 segments.
sns.histplot(y_pred, color='red', alpha=0.5, bins=50)
sns.histplot(y_train, color='blue', alpha=0.5, bins=50)
<AxesSubplot:ylabel='Count'>
We can see in the plot that our predicted prices are lower than actual prices and the mean of the prices peak is also low. Even though our model isn’t perfect we can use it to evaluate other models against it.
2.9 Root mean squared error¶
The RMSE is a measure of the error associated with a model for regression tasks. The video explained the RMSE formula in detail and implemented it in Python. This will be how we quanitfy the accuracy of the previous built model.
def rmse(y, y_pred):
se = (y - y_pred) ** 2
mse = se.mean()
return np.sqrt(mse)
rmse(y_train, y_pred)
0.7554192603920132
2.10 Using RMSE on validation data¶
Calculation of the RMSE on validation partition of the dataset of car price prediction. In this way, we have a metric to evaluate the model’s performance. The code below is what we needed to train our model on the X_train dataset, now we will set it up to train on the validation set that we created earlier in this notebook.
base = ['engine_hp', 'engine_cylinders', 'highway_mpg',
'city_mpg', 'popularity']
X_train = df_train[base].fillna(0).values
w0, w = train_linear_regression(X_train, y_train)
y_pred = w0 + X_train.dot(w)
def prepare_X(df):
df_num = df[base]
df_num = df_num.fillna(0)
X = df_num.values
return X
# Predicting on the training data set
X_train = prepare_X(df_train)
w0, w = train_linear_regression(X_train, y_train)
# Predicting on the validation data set
X_val = prepare_X(df_val)
y_pred = w0 + X_val.dot(w)
rmse(y_val, y_pred)
0.7616530991301601
2.11 Feature engineering¶
The feature age of the car was included in the dataset, obtained with the subtraction of the maximum year of cars and each of the years of cars. This new feature improved the model performance, measured with the RMSE and comparing the distributions of y target variable and predictions.
df_train
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | chevrolet | cobalt | 2008 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 2.0 | NaN | compact | coupe | 33 | 24 | 1385 |
| 1 | toyota | matrix | 2012 | regular_unleaded | 132.0 | 4.0 | automatic | front_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 32 | 25 | 2031 |
| 2 | subaru | impreza | 2016 | regular_unleaded | 148.0 | 4.0 | automatic | all_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 37 | 28 | 640 |
| 3 | volkswagen | vanagon | 1991 | regular_unleaded | 90.0 | 4.0 | manual | rear_wheel_drive | 3.0 | NaN | large | passenger_minivan | 18 | 16 | 873 |
| 4 | ford | f-150 | 2017 | flex-fuel_(unleaded/e85) | 385.0 | 8.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | crew_cab_pickup | 21 | 15 | 5657 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 7145 | bmw | 4_series | 2015 | premium_unleaded_(required) | 300.0 | 6.0 | automatic | rear_wheel_drive | 2.0 | luxury,performance | midsize | convertible | 31 | 20 | 3916 |
| 7146 | volkswagen | beetle | 2015 | premium_unleaded_(recommended) | 210.0 | 4.0 | automated_manual | front_wheel_drive | 2.0 | hatchback,performance | compact | 2dr_hatchback | 30 | 24 | 873 |
| 7147 | gmc | sierra_1500 | 2015 | flex-fuel_(unleaded/e85) | 285.0 | 6.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | extended_cab_pickup | 22 | 17 | 549 |
| 7148 | rolls-royce | ghost | 2014 | premium_unleaded_(required) | 563.0 | 12.0 | automatic | rear_wheel_drive | 4.0 | exotic,luxury,performance | large | sedan | 21 | 13 | 86 |
| 7149 | volkswagen | cc | 2017 | premium_unleaded_(recommended) | 200.0 | 4.0 | automated_manual | front_wheel_drive | 4.0 | performance | midsize | sedan | 31 | 22 | 873 |
7150 rows × 15 columns
The age of a car is a good prediction of price. The older the car the lower the price. We can calculate the age of the car by subtracing the year of the car from the max() year in the dataset.
df_train.year.max()
2017
2017 - df_train.year
0 9
1 5
2 1
3 26
4 0
..
7145 2
7146 2
7147 2
7148 3
7149 0
Name: year, Length: 7150, dtype: int64
We can use the function we created earlier and modify it to add the column ‘age’ as one of the features in our dataset.
def prepare_X(df):
df = df.copy() # create a copy so we are not modifying the original
df['age'] = 2017 - df.year # here we create the 'age' column.
features = base + ['age']# here we add the 'age' column to our base features.
df_num = df[features]
df_num = df_num.fillna(0)
X = df_num.values
return X
X_train = prepare_X(df_train)
X_train
array([[1.480e+02, 4.000e+00, 3.300e+01, 2.400e+01, 1.385e+03, 9.000e+00],
[1.320e+02, 4.000e+00, 3.200e+01, 2.500e+01, 2.031e+03, 5.000e+00],
[1.480e+02, 4.000e+00, 3.700e+01, 2.800e+01, 6.400e+02, 1.000e+00],
...,
[2.850e+02, 6.000e+00, 2.200e+01, 1.700e+01, 5.490e+02, 2.000e+00],
[5.630e+02, 1.200e+01, 2.100e+01, 1.300e+01, 8.600e+01, 3.000e+00],
[2.000e+02, 4.000e+00, 3.100e+01, 2.200e+01, 8.730e+02, 0.000e+00]])
After we run our predictions again we can see the RMSE decreased from 0.7554192603920132 down to 0.5172055461058329. The smaller the RMSE number is the closer our predictions are to the known prices.
# Predicting on the training data set
X_train = prepare_X(df_train)
w0, w = train_linear_regression(X_train, y_train)
# Predicting on the validation data set
X_val = prepare_X(df_val)
y_pred = w0 + X_val.dot(w)
rmse(y_val, y_pred)
0.5172055461058335
Visually we can see the graph is closer to the known prices.
sns.histplot(y_pred, color='red', alpha=0.5, bins=50)
sns.histplot(y_val, color='blue', alpha=0.5, bins=50)
<AxesSubplot:ylabel='Count'>
We are getting closer, there looks to be an issue with some of the lower priced cars.
2.12 Categorical variables¶
Categorical variables are typically strings, and pandas identify them as object types. These variables need to be converted to a numerical form because the ML models can interpret only numerical features. It is possible to incorporate certain categories from a feature, not necessarily all of them. This transformation from categorical to numerical variables is known as One-Hot encoding.
for v in [2, 3, 4]:
# ''%s' is used as a place holder for formatting strings and the '% v'
# will take the v iterable and replace the s in the '%s'
# the line below is creating a new column (feature) with the 'num_doors_2, 3 and 4'
# that will contain binary code to signify whether a records has that many doors.
# so where a records has 3 doors, there will be a 0 in the 2 column, 1 in the 3 column
# and 0 in the 4 column and then it is converted from boolean to an integer.
df_train['num_doors_%s' % v] = (df_train.number_of_doors == v).astype('int')
def prepare_X(df):
df = df.copy() # create a copy so we are not modifying the original
features = base.copy()
df['age'] = 2017 - df.year # here we create the 'age' column.
features.append('age')
for v in [2, 3, 4]:
# ''%s' is used as a place holder for formatting strings and the '% v'
# will take the v iterable and replace the s in the '%s'
# the line below is creating a new column (feature) with the 'num_doors_2, 3 and 4'
# that will contain binary code to signify whether a records has that many doors.
# so where a records has 3 doors, there will be a 0 in the 2 column, 1 in the 3 column
# and 0 in the 4 column and then it is converted from boolean to an integer.
df['num_doors_%s' % v] = (df.number_of_doors == v).astype('int')
features.append('num_doors_%s' % v)
df_num = df[features]
df_num = df_num.fillna(0)
X = df_num.values
return X
prepare_X(df_train)
array([[148., 4., 33., ..., 1., 0., 0.],
[132., 4., 32., ..., 0., 0., 1.],
[148., 4., 37., ..., 0., 0., 1.],
...,
[285., 6., 22., ..., 0., 0., 1.],
[563., 12., 21., ..., 0., 0., 1.],
[200., 4., 31., ..., 0., 0., 1.]])
Above we can see that our ‘prepare’ function added our categorical columns for number of doors.
# Predicting on the training data set
X_train = prepare_X(df_train)
w0, w = train_linear_regression(X_train, y_train)
# Predicting on the validation data set
X_val = prepare_X(df_val)
y_pred = w0 + X_val.dot(w)
rmse(y_val, y_pred)
0.5157995641502352
There is a very slight improvement using doors as a feature. Let’s look at adding the ‘Make’ as a feature.
makes = list(df.make.value_counts().head().index)
makes
['chevrolet', 'ford', 'volkswagen', 'toyota', 'dodge']
def prepare_X(df):
df = df.copy() # create a copy so we are not modifying the original
features = base.copy()
df['age'] = 2017 - df.year # here we create the 'age' column.
features.append('age')
for v in [2, 3, 4]:
# ''%s' is used as a place holder for formatting strings and the '% v'
# will take the v iterable and replace the s in the '%s'
# the line below is creating a new column (feature) with the 'num_doors_2, 3 and 4'
# that will contain binary code to signify whether a records has that many doors.
# so where a records has 3 doors, there will be a 0 in the 2 column, 1 in the 3 column
# and 0 in the 4 column and then it is converted from boolean to an integer.
df['num_doors_%s' % v] = (df.number_of_doors == v).astype('int')
features.append('num_doors_%s' % v)
for v in makes:
df['make_%s' % v] = (df.make == v).astype('int')
features.append('make_%s' % v)
df_num = df[features]
df_num = df_num.fillna(0)
X = df_num.values
return X
# Predicting on the training data set
X_train = prepare_X(df_train)
w0, w = train_linear_regression(X_train, y_train)
# Predicting on the validation data set
X_val = prepare_X(df_val)
y_pred = w0 + X_val.dot(w)
rmse(y_val, y_pred)
0.5076038849557034
As we can see, that made another slight improvement to our model by increasing it’s accuracy a little more.
df_train.dtypes
make object model object year int64 engine_fuel_type object engine_hp float64 engine_cylinders float64 transmission_type object driven_wheels object number_of_doors float64 market_category object vehicle_size object vehicle_style object highway_mpg int64 city_mpg int64 popularity int64 num_doors_2 int32 num_doors_3 int32 num_doors_4 int32 dtype: object
categorical_variables= [
'make', 'engine_fuel_type', 'transmission_type', 'driven_wheels',
'market_category', 'vehicle_size', 'vehicle_style'
]
categories = {}
for c in categorical_variables:
categories[c] = list(df[c].value_counts().head().index)
categories
{'make': ['chevrolet', 'ford', 'volkswagen', 'toyota', 'dodge'],
'engine_fuel_type': ['regular_unleaded',
'premium_unleaded_(required)',
'premium_unleaded_(recommended)',
'flex-fuel_(unleaded/e85)',
'diesel'],
'transmission_type': ['automatic',
'manual',
'automated_manual',
'direct_drive',
'unknown'],
'driven_wheels': ['front_wheel_drive',
'rear_wheel_drive',
'all_wheel_drive',
'four_wheel_drive'],
'market_category': ['crossover',
'flex_fuel',
'luxury',
'luxury,performance',
'hatchback'],
'vehicle_size': ['compact', 'midsize', 'large'],
'vehicle_style': ['sedan',
'4dr_suv',
'coupe',
'convertible',
'4dr_hatchback']}
def prepare_X(df):
df = df.copy() # create a copy so we are not modifying the original
features = base.copy()
df['age'] = 2017 - df.year # here we create the 'age' column.
features.append('age')
for v in [2, 3, 4]:
# ''%s' is used as a place holder for formatting strings and the '% v'
# will take the v iterable and replace the s in the '%s'
# the line below is creating a new column (feature) with the 'num_doors_2, 3 and 4'
# that will contain binary code to signify whether a records has that many doors.
# so where a records has 3 doors, there will be a 0 in the 2 column, 1 in the 3 column
# and 0 in the 4 column and then it is converted from boolean to an integer.
df['num_doors_%s' % v] = (df.number_of_doors == v).astype('int')
features.append('num_doors_%s' % v)
for c, values in categories.items():
for v in values:
df['%s_%s' % (c, v)] = (df[c] == v).astype('int')
features.append('%s_%s' % (c, v))
df_num = df[features]
df_num = df_num.fillna(0)
X = df_num.values
return X
prepare_X(df_train)
array([[148., 4., 33., ..., 1., 0., 0.],
[132., 4., 32., ..., 0., 0., 1.],
[148., 4., 37., ..., 0., 0., 1.],
...,
[285., 6., 22., ..., 0., 0., 0.],
[563., 12., 21., ..., 0., 0., 0.],
[200., 4., 31., ..., 0., 0., 0.]])
# Predicting on the training data set
X_train = prepare_X(df_train)
w0, w = train_linear_regression(X_train, y_train)
# Predicting on the validation data set
X_val = prepare_X(df_val)
y_pred = w0 + X_val.dot(w)
rmse(y_val, y_pred)
30.95303534636814
w0, w
(1.0988239383087294e+16,
array([ 2.57718953e-01, -1.19934338e+01, 3.82516348e-01, 3.02111785e+00,
-1.53845377e-03, 1.21209125e+00, 1.91949857e+03, 1.93164538e+03,
1.90555760e+03, -3.69174147e+00, 8.68736088e-01, 7.64802567e+00,
-8.43561473e+00, 2.31619373e+00, 1.31628092e+02, 1.15952480e+02,
1.21941647e+02, 1.29232893e+02, 1.15296794e+02, -8.45903444e+15,
-8.45903444e+15, -8.45903444e+15, -8.45903444e+15, -8.45903444e+15,
-2.52920494e+15, -2.52920494e+15, -2.52920494e+15, -2.52920494e+15,
3.10643155e+00, 4.16776654e+00, -4.10798492e-01, -4.66244197e+00,
-1.26472134e+01, 9.18260122e+00, 1.26076280e+01, 1.73773329e+01,
-4.85492239e-02, 5.44797374e-02, 1.78241160e-01, 3.41906701e-01,
-1.64412078e-01]))
2.13 Regularization¶
If the feature matrix has duplicated columns, it does not have an inverse matrix. But, sometimes this error could be passed if certain values are slightly different between duplicated columns.
So, if we apply the normal equation with this feature matrix, the values associated with duplicated columns are very large, which decreases the model performance. To solve this issue, one alternative is adding a small number to the diagonal of the feature matrix, which corresponds to regularization.
This technique works because the addition of small values to the diagonal makes it less likely to have duplicated columns. The regularization value is a parameter of the model. After applying regularization the model performance improved.
def train_linear_regression_reg(X, y, r=0.001):
ones = np.ones(X.shape[0])
X = np.column_stack([ones, X])
XTX = X.T.dot(X)
XTX = XTX + r * np.eye(XTX.shape[0])
XTX_inv = np.linalg.inv(XTX)
w_full = XTX_inv.dot(X.T).dot(y)
return w_full[0], w_full[1:]
# Predicting on the training data set
X_train = prepare_X(df_train)
w0, w = train_linear_regression_reg(X_train, y_train, r=0.01)
# Predicting on the validation data set
X_val = prepare_X(df_val)
y_pred = w0 + X_val.dot(w)
rmse(y_val, y_pred)
0.45652199012705297
2.14 Tuning the model¶
The tuning consisted of finding the best regularization value, using the validation partition of the dataset. After obtaining the best regularization value, the model was trained with this regularization parameter.
for r in [0.0, 0.00001, 0.0001, 0.001, 0.1, 1, 10]:
# Predicting on the training data set
X_train = prepare_X(df_train)
w0, w = train_linear_regression_reg(X_train, y_train, r=r)
# Predicting on the validation data set
X_val = prepare_X(df_val)
y_pred = w0 + X_val.dot(w)
score = rmse(y_val, y_pred)
print(r, w0, score)
0.0 1.0988239383087294e+16 30.95303534636814 1e-05 9.263833450169736 0.45651701545049306 0.0001 6.330946383506262 0.45651706300621603 0.001 6.285522284126121 0.456517508702663 0.1 6.191208657252675 0.45656927630429756 1 5.634896667950106 0.45722043179967253 10 4.283980108969658 0.47014569320991684
r = 0.001
X_train = prepare_X(df_train)
w0, w = train_linear_regression_reg(X_train, y_train, r=r)
# Predicting on the validation data set
X_val = prepare_X(df_val)
y_pred = w0 + X_val.dot(w)
score = rmse(y_val, y_pred)
print(r, w0, score)
0.001 6.285522284126121 0.456517508702663
2.15 Using the model¶
After finding the best model and its parameters, it was trained with training and validation partitions and the final evaluation was calculated on the test partition. Finally, the final model was used to predict the price of new cars.
Now that we validated our model with the validation set, it can be added back in with the training data set so that we have one large training set, which comprises 80% of the original dataset.
df_full_train = pd.concat([df_train, df_val])
df_full_train
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | num_doors_2 | num_doors_3 | num_doors_4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | chevrolet | cobalt | 2008 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 2.0 | NaN | compact | coupe | 33 | 24 | 1385 | 1.0 | 0.0 | 0.0 |
| 1 | toyota | matrix | 2012 | regular_unleaded | 132.0 | 4.0 | automatic | front_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 32 | 25 | 2031 | 0.0 | 0.0 | 1.0 |
| 2 | subaru | impreza | 2016 | regular_unleaded | 148.0 | 4.0 | automatic | all_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 37 | 28 | 640 | 0.0 | 0.0 | 1.0 |
| 3 | volkswagen | vanagon | 1991 | regular_unleaded | 90.0 | 4.0 | manual | rear_wheel_drive | 3.0 | NaN | large | passenger_minivan | 18 | 16 | 873 | 0.0 | 1.0 | 0.0 |
| 4 | ford | f-150 | 2017 | flex-fuel_(unleaded/e85) | 385.0 | 8.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | crew_cab_pickup | 21 | 15 | 5657 | 0.0 | 0.0 | 1.0 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 2377 | volvo | v60 | 2015 | regular_unleaded | 240.0 | 4.0 | automatic | front_wheel_drive | 4.0 | luxury | midsize | wagon | 37 | 25 | 870 | NaN | NaN | NaN |
| 2378 | maserati | granturismo_convertible | 2015 | premium_unleaded_(required) | 444.0 | 8.0 | automatic | rear_wheel_drive | 2.0 | exotic,luxury,high-performance | midsize | convertible | 20 | 13 | 238 | NaN | NaN | NaN |
| 2379 | cadillac | escalade_hybrid | 2013 | regular_unleaded | 332.0 | 8.0 | automatic | rear_wheel_drive | 4.0 | luxury,hybrid | large | 4dr_suv | 23 | 20 | 1624 | NaN | NaN | NaN |
| 2380 | mitsubishi | lancer | 2016 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 4.0 | NaN | compact | sedan | 34 | 24 | 436 | NaN | NaN | NaN |
| 2381 | kia | sorento | 2015 | regular_unleaded | 290.0 | 6.0 | automatic | front_wheel_drive | 4.0 | crossover | midsize | 4dr_suv | 25 | 18 | 1720 | NaN | NaN | NaN |
9532 rows × 18 columns
Above we can see that there are 9532 rows but the index is still set from the validation dataset so we will reset the index.
df_full_train = df_full_train.reset_index(drop=True)
df_full_train
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | num_doors_2 | num_doors_3 | num_doors_4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | chevrolet | cobalt | 2008 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 2.0 | NaN | compact | coupe | 33 | 24 | 1385 | 1.0 | 0.0 | 0.0 |
| 1 | toyota | matrix | 2012 | regular_unleaded | 132.0 | 4.0 | automatic | front_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 32 | 25 | 2031 | 0.0 | 0.0 | 1.0 |
| 2 | subaru | impreza | 2016 | regular_unleaded | 148.0 | 4.0 | automatic | all_wheel_drive | 4.0 | hatchback | compact | 4dr_hatchback | 37 | 28 | 640 | 0.0 | 0.0 | 1.0 |
| 3 | volkswagen | vanagon | 1991 | regular_unleaded | 90.0 | 4.0 | manual | rear_wheel_drive | 3.0 | NaN | large | passenger_minivan | 18 | 16 | 873 | 0.0 | 1.0 | 0.0 |
| 4 | ford | f-150 | 2017 | flex-fuel_(unleaded/e85) | 385.0 | 8.0 | automatic | four_wheel_drive | 4.0 | flex_fuel | large | crew_cab_pickup | 21 | 15 | 5657 | 0.0 | 0.0 | 1.0 |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 9527 | volvo | v60 | 2015 | regular_unleaded | 240.0 | 4.0 | automatic | front_wheel_drive | 4.0 | luxury | midsize | wagon | 37 | 25 | 870 | NaN | NaN | NaN |
| 9528 | maserati | granturismo_convertible | 2015 | premium_unleaded_(required) | 444.0 | 8.0 | automatic | rear_wheel_drive | 2.0 | exotic,luxury,high-performance | midsize | convertible | 20 | 13 | 238 | NaN | NaN | NaN |
| 9529 | cadillac | escalade_hybrid | 2013 | regular_unleaded | 332.0 | 8.0 | automatic | rear_wheel_drive | 4.0 | luxury,hybrid | large | 4dr_suv | 23 | 20 | 1624 | NaN | NaN | NaN |
| 9530 | mitsubishi | lancer | 2016 | regular_unleaded | 148.0 | 4.0 | manual | front_wheel_drive | 4.0 | NaN | compact | sedan | 34 | 24 | 436 | NaN | NaN | NaN |
| 9531 | kia | sorento | 2015 | regular_unleaded | 290.0 | 6.0 | automatic | front_wheel_drive | 4.0 | crossover | midsize | 4dr_suv | 25 | 18 | 1720 | NaN | NaN | NaN |
9532 rows × 18 columns
Now that we have concatenated the train and val set back together and reset the index we can now use our previously built prepare_X function to prepare the new entire training set.
X_full_train = prepare_X(df_full_train)
X_full_train
array([[148., 4., 33., ..., 1., 0., 0.],
[132., 4., 32., ..., 0., 0., 1.],
[148., 4., 37., ..., 0., 0., 1.],
...,
[332., 8., 23., ..., 0., 0., 0.],
[148., 4., 34., ..., 0., 0., 0.],
[290., 6., 25., ..., 0., 0., 0.]])
We also need to concatenate the y’s together.
y_full_train = np.concatenate([y_train, y_val])
y_full_train
array([ 9.57574708, 9.887663 , 9.89323518, ..., 11.21756062,
9.77542688, 10.1924563 ])
w0, w = train_linear_regression_reg(X_full_train, y_full_train, r=0.001)
w0, w
(6.321897140639891,
array([ 1.52506334e-03, 1.18188694e-01, -6.66105724e-03, -5.33414117e-03,
-4.87603196e-05, -9.69091849e-02, -7.92623108e-01, -8.90864322e-01,
-6.35103033e-01, -4.14339218e-02, 1.75560737e-01, -5.78067084e-04,
-1.00563873e-01, -9.27549683e-02, -4.66859089e-01, 7.98659955e-02,
-3.16047638e-01, -5.51981604e-01, -7.89525255e-02, 1.09536726e+00,
9.20059720e-01, 1.14963711e+00, 2.65277321e+00, 5.09996289e-01,
1.62933899e+00, 1.53004304e+00, 1.61722175e+00, 1.54522114e+00,
-9.70559788e-02, 3.73062078e-02, -5.81767461e-02, -2.35940808e-02,
-1.19357029e-02, 2.18895262e+00, 2.07458271e+00, 2.05916687e+00,
-5.00802769e-02, 5.62184639e-02, 1.84794024e-01, 3.32646151e-01,
-1.58817038e-01]))
X_test = prepare_X(df_test)
y_pred = w0 + X_test.dot(w)
score = rmse(y_test, y_pred)
score
0.45177493042600725
Now our model has been created, we want to try it on some of the cars in our dataset. We picked the car with index 20 and we want to convert the data for that car into a dictionary just as a website might send the data.
car = df_test.iloc[20].to_dict()
car
{'make': 'toyota',
'model': 'sienna',
'year': 2015,
'engine_fuel_type': 'regular_unleaded',
'engine_hp': 266.0,
'engine_cylinders': 6.0,
'transmission_type': 'automatic',
'driven_wheels': 'front_wheel_drive',
'number_of_doors': 4.0,
'market_category': nan,
'vehicle_size': 'large',
'vehicle_style': 'passenger_minivan',
'highway_mpg': 25,
'city_mpg': 18,
'popularity': 2031}
Now, since we need a dataframe to plug into our model, we will convert the dictionary sent from the website to a dataframe.
df_small = pd.DataFrame([car])
df_small
| make | model | year | engine_fuel_type | engine_hp | engine_cylinders | transmission_type | driven_wheels | number_of_doors | market_category | vehicle_size | vehicle_style | highway_mpg | city_mpg | popularity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | toyota | sienna | 2015 | regular_unleaded | 266.0 | 6.0 | automatic | front_wheel_drive | 4.0 | NaN | large | passenger_minivan | 25 | 18 | 2031 |
Now we use our prepare_X function to generate our weights.
X_small = prepare_X(df_small)
X_small
array([[2.660e+02, 6.000e+00, 2.500e+01, 1.800e+01, 2.031e+03, 2.000e+00,
0.000e+00, 0.000e+00, 1.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
1.000e+00, 0.000e+00, 1.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 1.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
1.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 1.000e+00,
0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 0.000e+00]])
With our weights generated we can see the prediction that our model creates.
y_pred = w0 + X_small.dot(w)
y_pred = y_pred[0]
y_pred
10.462651726547548
Remember, our model was converted to a log scale, which we have to undo here to get a dollar amount.
np.expm1(y_pred)
34983.19708133757
Let’s do the same thing to the actual values, and we can see that our model is very, very close.
np.expm1(y_test[20])
35000.00000000001
2.16 Car price prediction project summary¶
In summary, this session covered some topics, including data preparation, exploratory data analysis, the validation framework, linear regression model, LR vector and normal forms, the baseline model, root mean squared error, feature engineering, regularization, tuning the model, and using the best model with new data. All these concepts were explained using the problem to predict the price of cars.
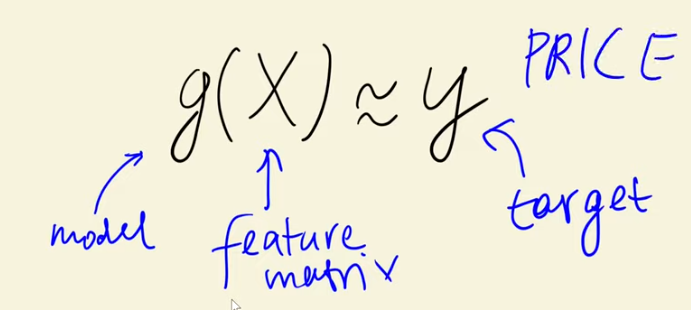
Leave a Reply